Simplify to a + bi: -2/(3 - i) * (5/i) =
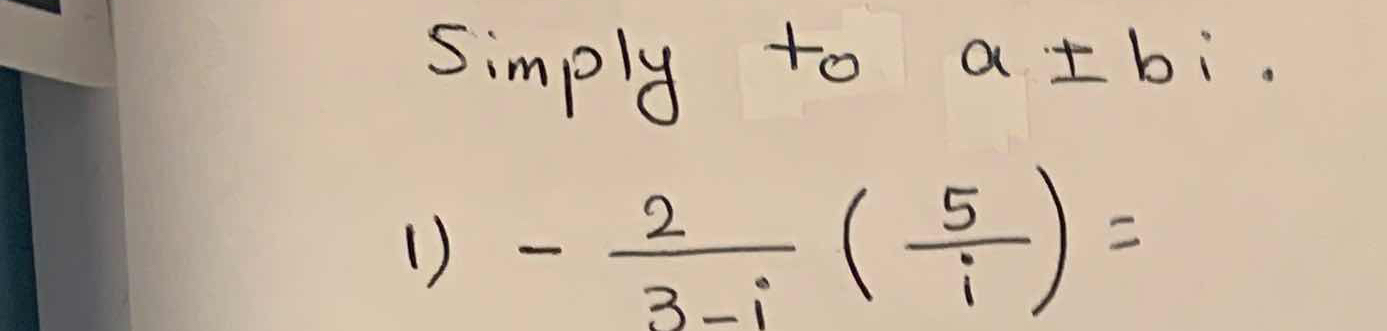
Understand the Problem
The question is asking for a simplification of a complex number expression into the form a + bi, where a and b are real numbers. It involves a fraction with complex denominators and requires the multiplication by a conjugate.
Answer
The final answer is $-1 + 3i$.
Answer for screen readers
The simplified expression is $-1 + 3i$.
Steps to Solve
- Multiply by the Conjugate of the Denominator
We first tackle the fraction $-\frac{2}{3 - i}$. To eliminate the complex denominator, we multiply both the numerator and the denominator by the conjugate of the denominator, which is $3 + i$:
$$ -\frac{2}{3 - i} \cdot \frac{3 + i}{3 + i} = -\frac{2(3 + i)}{(3 - i)(3 + i)} $$
- Simplify the Denominator
Next, we simplify the denominator using the difference of squares:
$$ (3 - i)(3 + i) = 3^2 - i^2 = 9 - (-1) = 9 + 1 = 10 $$
Thus, our expression now becomes:
$$ -\frac{2(3 + i)}{10} $$
- Simplify the Expression
Now we can simplify the fraction:
$$ -\frac{2(3 + i)}{10} = -\frac{6 + 2i}{10} = -\frac{3}{5} - \frac{1}{5} i $$
- Multiply the Whole Expression by $5/i$
Next, we multiply our result by $\frac{5}{i}$:
$$ \left(-\frac{3}{5} - \frac{1}{5} i\right) \cdot \frac{5}{i} $$
- Distribute the Terms
Distributing yields:
$$ -\frac{3}{5} \cdot \frac{5}{i} - \frac{1}{5} i \cdot \frac{5}{i} $$
This simplifies to:
$$ -\frac{3}{i} - 1 $$
- Rewrite $\frac{3}{i}$
To express $-\frac{3}{i}$ in standard form, multiply by $\frac{i}{i}$:
$$ -\frac{3}{i} = -3 \cdot \frac{i}{i^2} = -3 \cdot \frac{i}{-1} = 3i $$
- Combine the Real and Imaginary Parts
Now we combine the simplified terms:
$$ 3i - 1 = -1 + 3i $$
Thus, we have the final result in the form $a + bi$.
The simplified expression is $-1 + 3i$.
More Information
This problem involves dealing with complex numbers and their conjugates. Using the conjugate helps to eliminate the imaginary unit from the denominator, making it possible to simplify the expression effectively.
Tips
- Forgetting to multiply both the numerator and denominator by the conjugate.
- Neglecting to multiply the entire expression by $\frac{5}{i}$ thoroughly.
- Misapplying operations leading to mistakes in simplifying complex fractions.
AI-generated content may contain errors. Please verify critical information