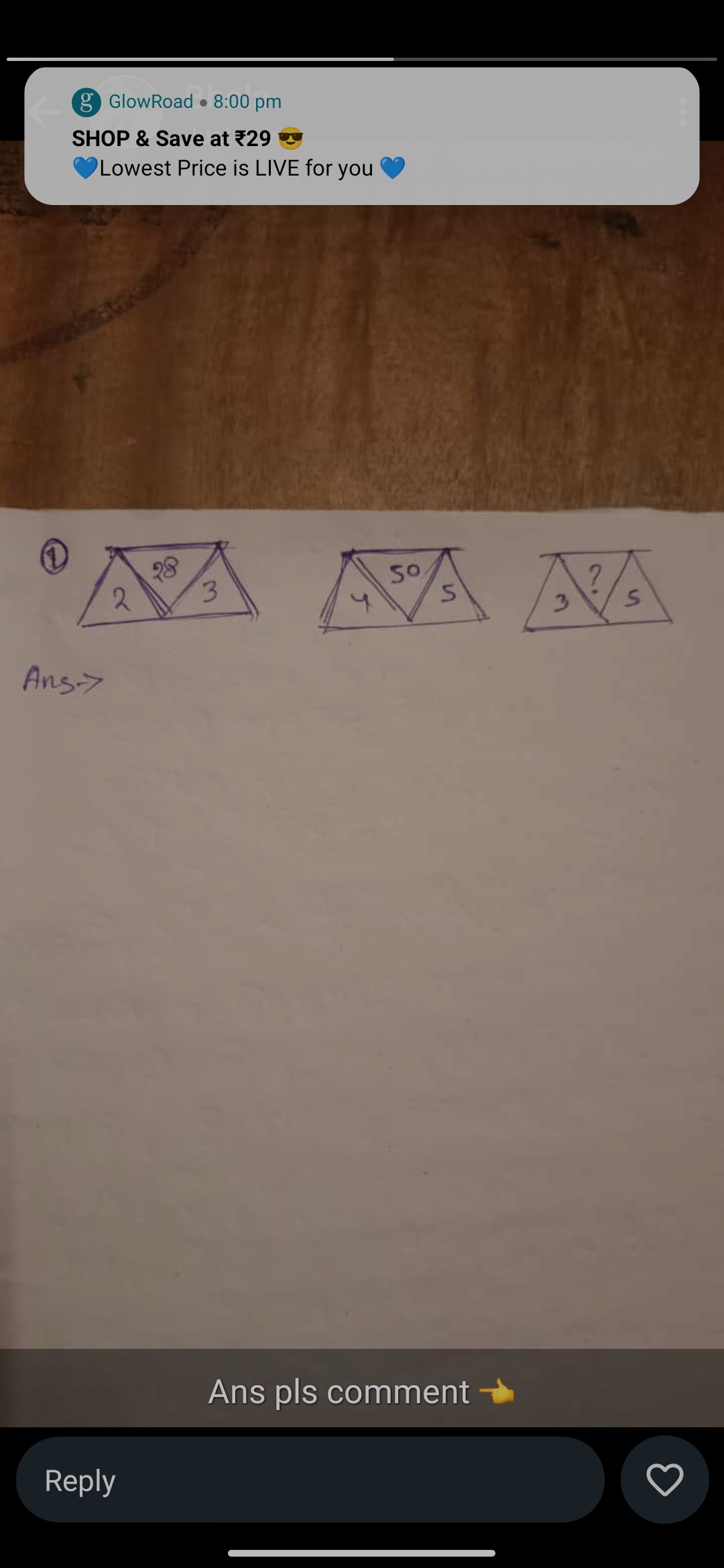
What is the missing value in the triangle puzzle shown in the image?

Steps to Solve

1. Identifying the relationship between the sides and angles of the triangles

In the given problem, the triangles appear to include values that relate to their angles (28° and 50°) and the lengths of their sides (2, 3; 4, 5; 3, 5). Observe the relationships to establish a pattern.

2. Analyzing the first triangle

For the left triangle:

• The two inner angles are represented as (28^\circ) and the corresponding sides are 2 and 3.

Using the sine rule:

$$ \frac{a}{\sin(A)} = \frac{b}{\sin(B)} $$

This helps to establish the ratio of sides to angles.

3. Setting up the second triangle

Looking at the second triangle (middle) with angles and sides of 50°, 4, and 5. Using the sine rule again:

• Let the opposite angle to side 4 be (x):

$$ \frac{4}{\sin(50^\circ)} = \frac{5}{\sin(x)} $$

4. Finding the unknown angle in the third triangle

In the third triangle, we need to determine the angle opposite to the side with (?).

Using the sine relationship from the previous triangles, we evaluate:

$$ \frac{3}{\sin(28^\circ)} = \frac{5}{\sin(?)} $$

5. Calculating the unknown angle

Rearranging the equation:

$$ \sin(?) = \frac{5 \cdot \sin(28^\circ)}{3} $$

Now, calculate the value of ( \sin(?) ).

6. Final Calculation Using Inverse Function

Using the inverse sine function, find the angle:

$$ ? = \sin^{-1}\left(\frac{5 \cdot \sin(28^\circ)}{3}\right) $$