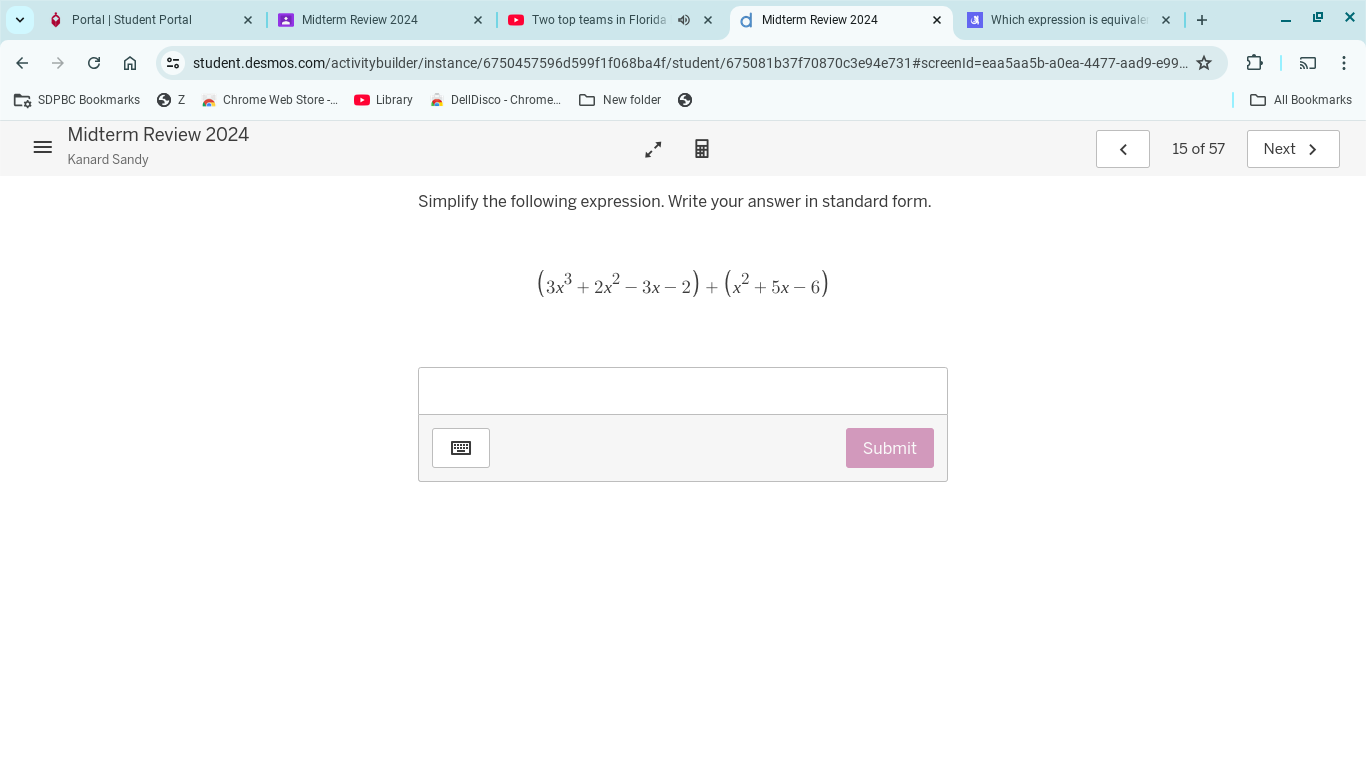
Simplify the following expression. Write your answer in standard form: (3x^3 + 2x^2 - 3x - 2) + (x^2 + 5x - 6)
Understand the Problem
The question is asking to simplify a given polynomial expression and write the answer in standard form. The expression consists of several polynomial terms that need to be combined.
Answer
The simplified expression in standard form is $$ 3x^3 + 3x^2 + 2x - 8 $$
Answer for screen readers
The simplified expression in standard form is
$$ 3x^3 + 3x^2 + 2x - 8 $$
Steps to Solve
- Identify the polynomials to combine
The expression to simplify is
$$ (3x^3 + 2x^2 - 3x - 2) + (x^2 + 5x - 6) $$
- Combine like terms
Group and combine the like terms from both polynomials:
- The $x^3$ terms: $3x^3$
- The $x^2$ terms: $2x^2 + x^2 = 3x^2$
- The $x$ terms: $-3x + 5x = 2x$
- The constant terms: $-2 - 6 = -8$
- Write the simplified expression
Now, combine all the results:
$$ 3x^3 + 3x^2 + 2x - 8 $$
- State the expression in standard form
The standard form is already achieved as the terms are ordered from highest degree to lowest degree.
The simplified expression in standard form is
$$ 3x^3 + 3x^2 + 2x - 8 $$
More Information
In polynomial expressions, combining like terms involves adding coefficients of the same degree. The highest degree term determines the leading term of the polynomial.
Tips
- Failing to combine all like terms.
- Forgetting to pay attention to the signs when adding or subtracting terms.
AI-generated content may contain errors. Please verify critical information