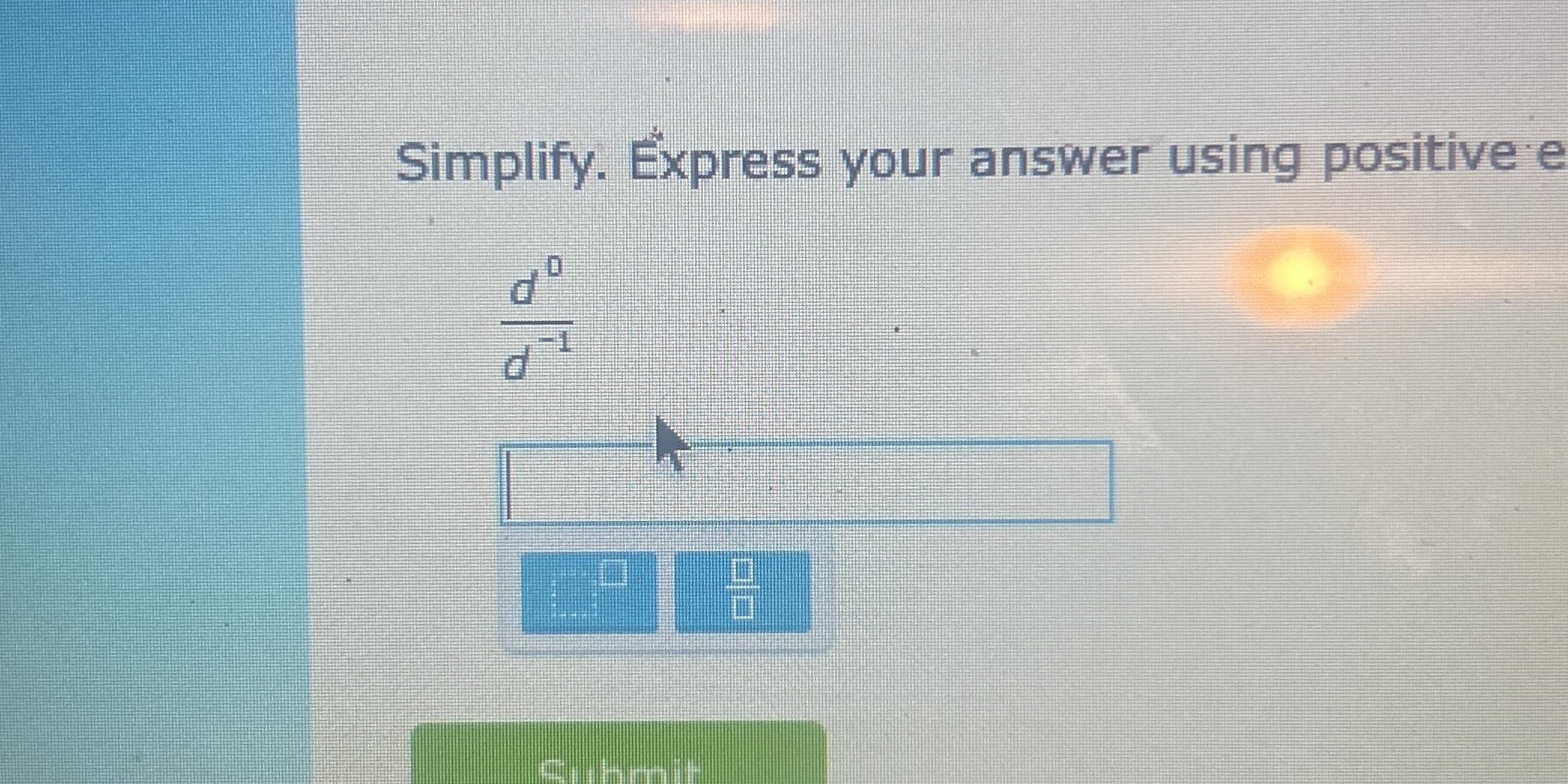
Simplify the expression \frac{y^0}{y^{-1}}.
Understand the Problem
The question is asking to simplify the expression wrapped in the fraction, which includes variables raised to certain powers, and to provide the answer using positive exponents.
Answer
The simplified expression is \( y \).
Answer for screen readers
The simplified expression is ( y ).
Steps to Solve
- Rewrite the expression Let's start with the original expression, which is
$$ \frac{d^0}{y^{-1}} $$
- Simplify the numerator According to the law of exponents, any non-zero number raised to the power of zero equals one. Thus, we can simplify the numerator:
$$ d^0 = 1 $$
- Simplify the denominator The denominator has a negative exponent. We can rewrite it using the positive exponent rule:
$$ y^{-1} = \frac{1}{y} \quad \text{or} \quad y^{-1} = \frac{1}{y} \implies \text{We will multiply by } y \text{ after rewriting} $$
- Combine the simplified terms Now we rewrite the overall expression:
$$ \frac{1}{y^{-1}} = 1 \cdot y = y \quad \text{(multiplying numerator by the reciprocal of the denominator)} $$
Thus, the final simplified expression is:
$$ y $$
The simplified expression is ( y ).
More Information
The expression simplifies to ( y ) because ( d^0 ) is always 1 for any non-zero ( d ), and the negative exponent ( y^{-1} ) is rewritten to its positive form. This process is a basic application of the rules of exponents.
Tips
- Misinterpreting ( d^0 ) as zero instead of simplifying it to 1.
- Forgetting to rewrite negative exponents as positive when simplifying.
AI-generated content may contain errors. Please verify critical information