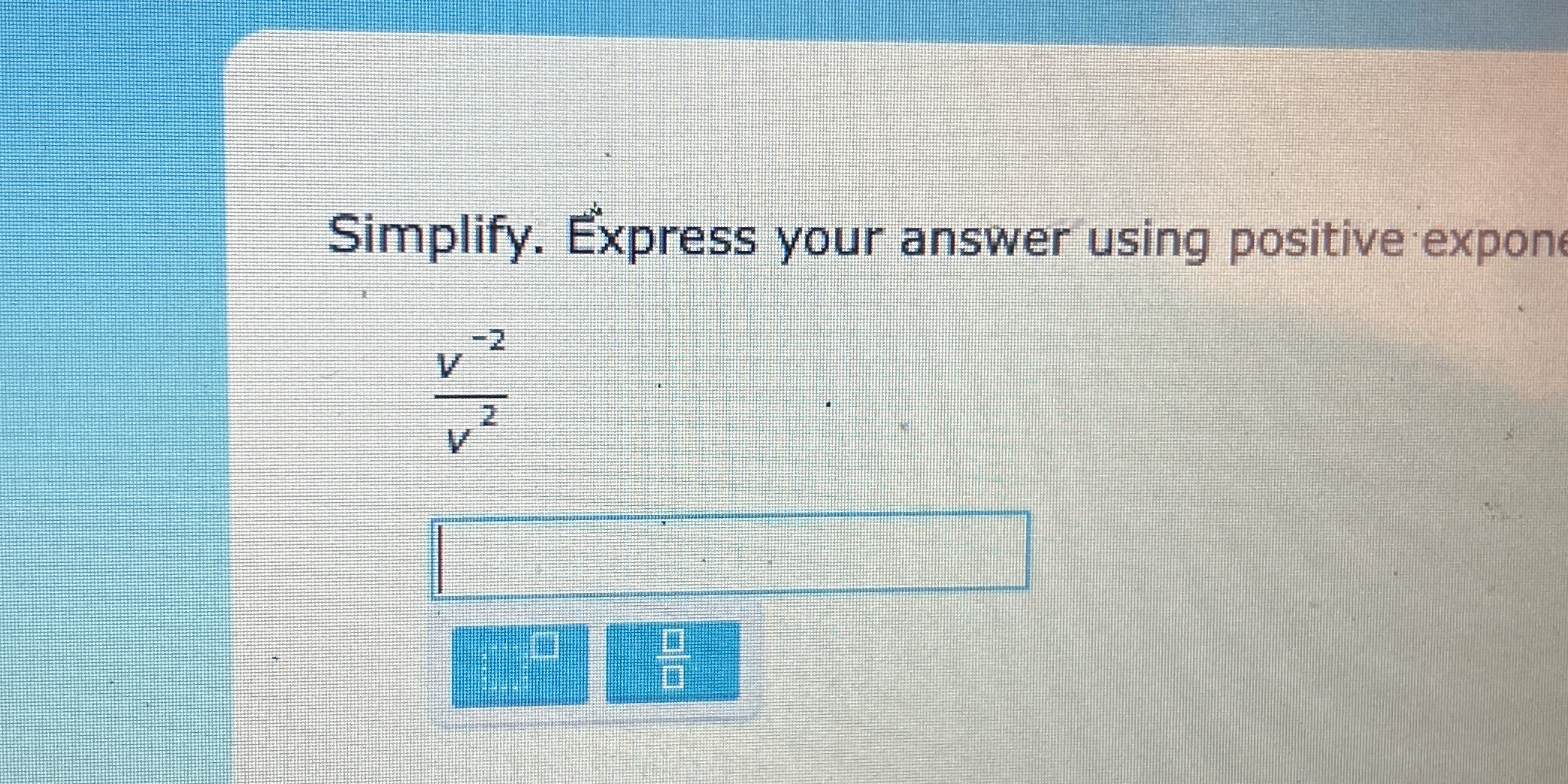
Simplify the expression \( \frac{\sqrt{-2}}{\sqrt{2}} \). Express your answer using positive exponents.
Understand the Problem
The question asks to simplify the expression given by the formula, which involves applying the properties of exponents and radicals to express the result using positive exponents.
Answer
$$ i $$
Answer for screen readers
$$ i $$
Steps to Solve
- Rewrite the expression
The given expression is
$$ \frac{\sqrt{-2}}{\sqrt{2}} $$
We can express the square roots as exponents. Thus, we rewrite it as:
$$ \frac{(-2)^{1/2}}{2^{1/2}} $$
- Apply the properties of exponents
Using the property that states
$$ \frac{a^m}{b^m} = \left(\frac{a}{b}\right)^m $$
we can simplify the expression:
$$ \frac{\sqrt{-2}}{\sqrt{2}} = \sqrt{\frac{-2}{2}} $$
- Simplify the fraction
Now simplify the fraction inside the square root:
$$ \frac{-2}{2} = -1 $$
So we can update the expression to:
$$ \sqrt{-1} $$
- Express in terms of imaginary unit
The square root of -1 is defined as the imaginary unit, denoted by $i$:
$$ \sqrt{-1} = i $$
Thus, the final simplified expression is:
$$ i $$
$$ i $$
More Information
The solution involves recognizing that the square root of a negative number introduces the imaginary unit, $i$, which is fundamental in complex number theory.
Tips
- Failing to recognize that taking the square root of a negative number leads to an imaginary number.
- Not applying exponent properties correctly when manipulating the expression.
AI-generated content may contain errors. Please verify critical information