Simplify (2x^5)^3
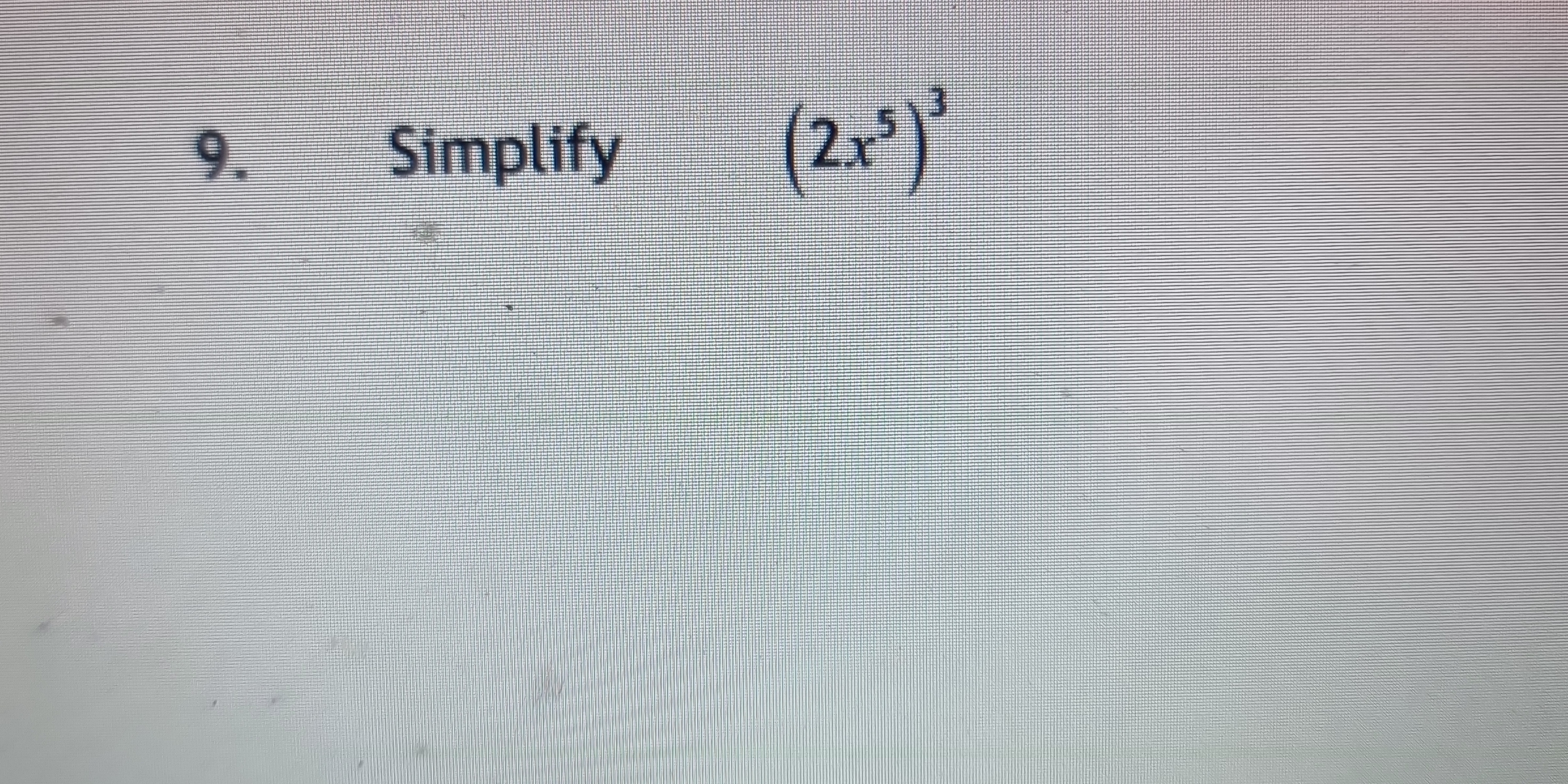
Understand the Problem
The question is asking to simplify the expression (2x^5)^3. We need to apply the power of a product rule and recognize how to simplify powers of variables and coefficients.
Answer
The simplified expression is $8x^{15}$.
Answer for screen readers
The simplified expression is $8x^{15}$.
Steps to Solve
-
Recognize the Power of a Product Rule We know that $(ab)^n = a^n b^n$. Here, we apply this to the expression $(2x^5)^3$.
-
Apply the Power to the Coefficient First, we simplify the coefficient: $$ (2)^3 = 8 $$
-
Apply the Power to the Variable Next, we raise the variable to the power: $$ (x^5)^3 = x^{5 \cdot 3} = x^{15} $$
-
Combine the Results Now combine the simplified coefficients and variables: $$ (2x^5)^3 = 8x^{15} $$
The simplified expression is $8x^{15}$.
More Information
This problem demonstrates the application of the power of a product rule and helps in understanding the manipulation of both coefficients and variables when simplifying expressions with powers.
Tips
- Forgetting to apply the power to both coefficients and variables: It's important to remember that both parts of the expression must be raised to the given power.
- Incorrectly multiplying the exponents: Ensure that when raising a power to another power, you multiply the exponents correctly.
AI-generated content may contain errors. Please verify critical information