Simplify the expression (2g^2n^2)(-7p^3r^4)^2(6pr^3)(5a^2b^3c^4)(6a^3b^4c^2).
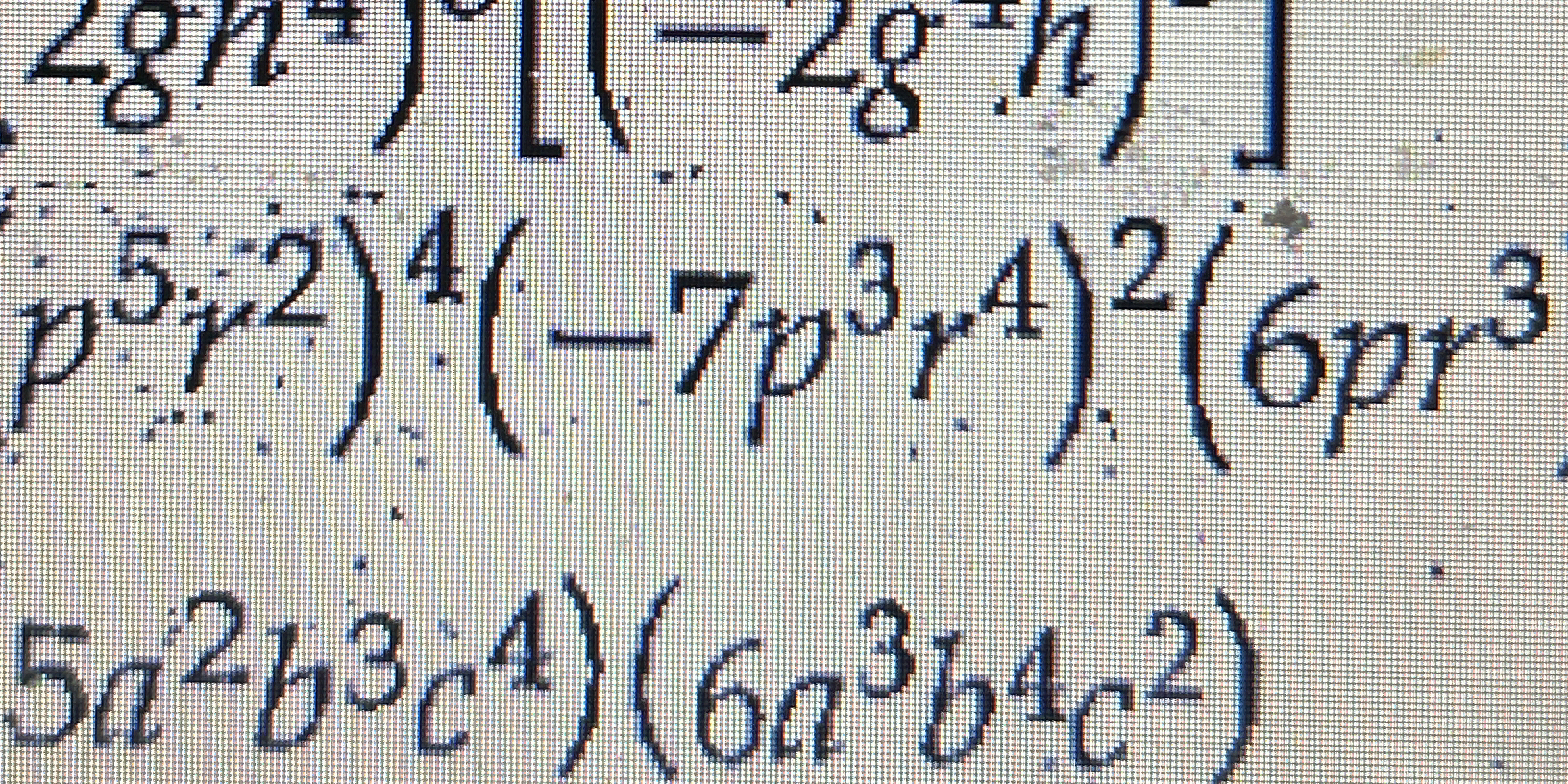
Understand the Problem
The question involves a calculus expression likely related to algebraic manipulation and polynomial expansion, where various terms with exponents need to be simplified or multiplied together.
Answer
The final expression is $17640g^2n^2p^{7}r^{11}a^{5}b^{7}c^{6}$.
Answer for screen readers
The final expression is $$ 17640g^2n^2p^{7}r^{11}a^{5}b^{7}c^{6}. $$
Steps to Solve
- Simplify each term Start with the individual terms:
- The first term is (2g^2n^2).
- The second term is ((-7p^3r^4)^2). Calculate this: $$ (-7)^2 \cdot (p^3)^2 \cdot (r^4)^2 = 49p^6r^8. $$
-
Calculate the third term The third term is (6pr^3), which remains as is.
-
Combine the fourth term The fourth term is (5a^2b^3c^4), which also remains unchanged.
-
Process the fifth term The fifth term is (6a^3b^4c^2), which stays the same.
-
Combine all terms together Now combine all simplified terms together: $$ (2g^2n^2) \cdot (49p^6r^8) \cdot (6pr^3) \cdot (5a^2b^3c^4) \cdot (6a^3b^4c^2). $$
-
Multiply the coefficients Multiply the numerical coefficients: $$ 2 \cdot 49 \cdot 6 \cdot 5 \cdot 6 = 2 \times 49 = 98,\ 98 \times 6 = 588,\ 588 \times 5 = 2940,\ 2940 \times 6 = 17640. $$
-
Combine like terms Now combine the variables:
- For (p): (p^6 \cdot p^1 = p^{7}),
- For (r): (r^8 \cdot r^3 = r^{11}),
- For (a): (a^2 \cdot a^3 = a^{5}),
- For (b): (b^3 \cdot b^4 = b^{7}),
- For (c): (c^4 \cdot c^2 = c^{6}).
- Write the final expression Combine everything into the final expression: $$ 17640g^2n^2p^{7}r^{11}a^{5}b^{7}c^{6}. $$
The final expression is $$ 17640g^2n^2p^{7}r^{11}a^{5}b^{7}c^{6}. $$
More Information
This expression combines various algebraic terms and demonstrates how to handle powers and coefficients systematically. Each basic polynomial was handled carefully to ensure no errors were made during the multiplication.
Tips
- Forgetting to square each component of an exponentiated term (e.g., ((-7p^3r^4)^2)).
- Not properly combining like terms, especially when there are many variables involved.
- Miscalculating numerical coefficients during multiplication.
AI-generated content may contain errors. Please verify critical information