Range of g(x) = { 6x + 7, x ≤ -2; 4x + 3, x > 2 } is:
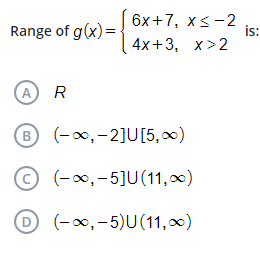
Understand the Problem
The question is asking for the range of a piecewise function defined as g(x) for two different intervals. We need to evaluate the function based on the specified conditions and determine what values g(x) can take.
Answer
The range of \( g(x) \) is \( (-\infty, -5] \cup [11, \infty) \).
Answer for screen readers
The range of ( g(x) ) is ( (-\infty, -5] \cup [11, \infty) ).
Steps to Solve
-
Evaluate the first piece of the function
The first part of the function is given by ( g(x) = 6x + 7 ) for ( x \leq -2 ).
To find the range, we first evaluate this expression at the boundary point: [ g(-2) = 6(-2) + 7 = -12 + 7 = -5 ] As ( x ) decreases towards negative infinity, ( g(x) ) also approaches negative infinity. Thus, the output values for this piece range from ( -5 ) to ( -\infty ).
-
Evaluate the second piece of the function
The second part of the function is defined as ( g(x) = 4x + 3 ) for ( x > 2 ).
We find the value of this part at the boundary point ( x = 2 ): [ g(2) = 4(2) + 3 = 8 + 3 = 11 ] As ( x ) increases towards positive infinity, ( g(x) ) goes toward positive infinity. Thus, the output values for this piece range from ( 11 ) to ( +\infty ).
-
Combine the two ranges
We now combine the ranges obtained from both pieces:
- From the first piece, the range is ( (-\infty, -5] ).
- From the second piece, the range is ( [11, +\infty) ).
Combining these, the overall range of ( g(x) ) is: [ (-\infty, -5] \cup [11, \infty) ]
The range of ( g(x) ) is ( (-\infty, -5] \cup [11, \infty) ).
More Information
The piecewise function combines two linear functions, and evaluating their individual ranges provides us with the overall range of the function. The function does not cover the interval ((-5, 11)) due to the linear nature of the segments.
Tips
- Forgetting the boundaries: Ensure that you evaluate the function at the boundary points correctly to obtain the exact range.
- Improper combination: Ensure you recognize that the piecewise nature results in two distinct ranges that must be expressed as a union.
AI-generated content may contain errors. Please verify critical information