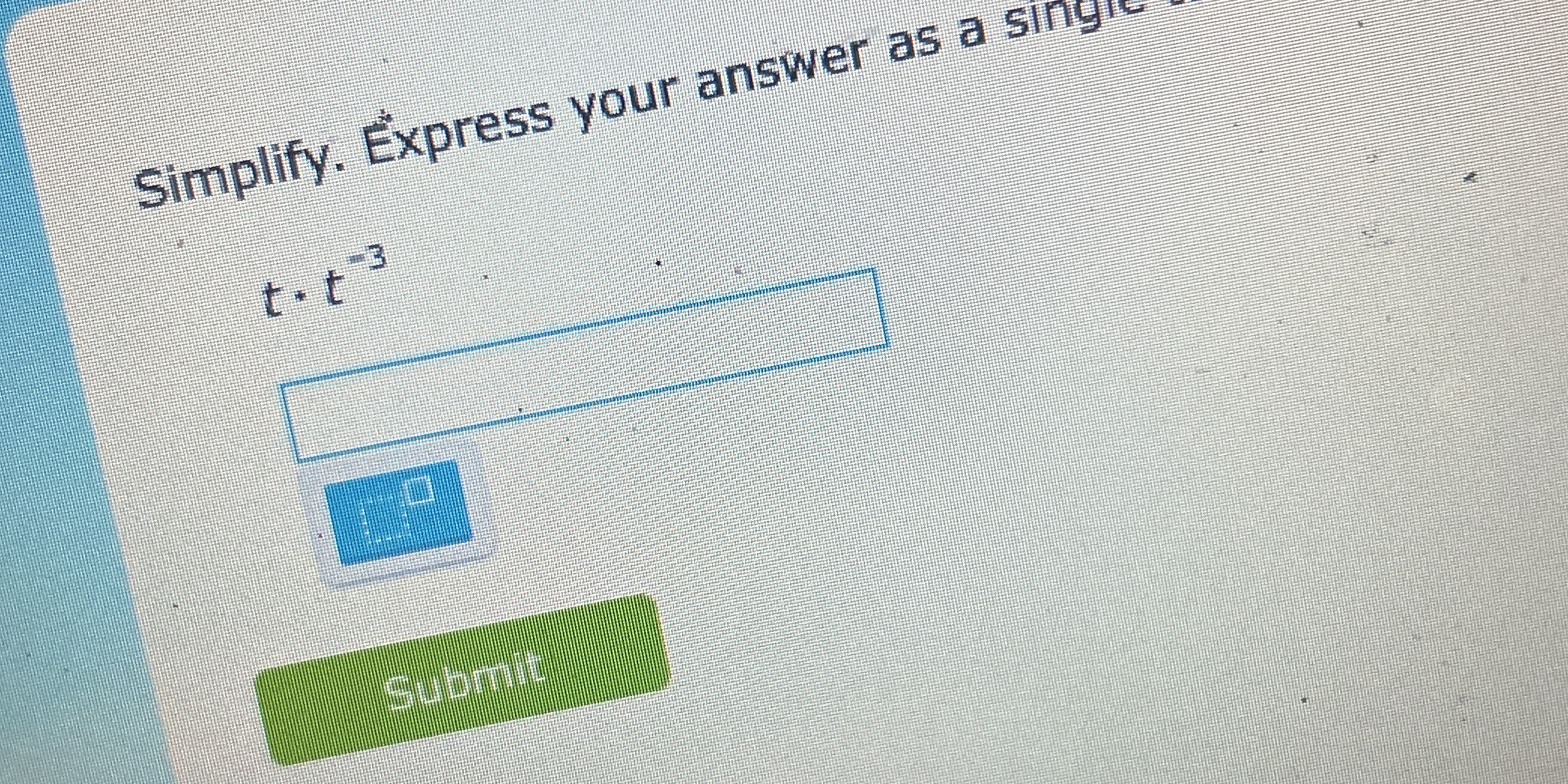
Simplify t * t^(-3).
Understand the Problem
The question is asking us to simplify the expression t * t^(-3). This involves applying the laws of exponents to combine the terms effectively.
Answer
The simplified expression is \( \frac{1}{t^2} \).
Answer for screen readers
The simplified expression is ( \frac{1}{t^2} ).
Steps to Solve
-
Identify the expression We start with the expression ( t \cdot t^{-3} ).
-
Apply the Laws of Exponents Using the property of exponents that states ( a^m \cdot a^n = a^{m+n} ), we combine the terms. Here, ( m = 1 ) and ( n = -3 ).
-
Combine the exponents Thus, we have: $$ t \cdot t^{-3} = t^{1 + (-3)} = t^{-2} $$
-
Rewrite the expression The expression ( t^{-2} ) can be rewritten using the definition of negative exponents: $$ t^{-2} = \frac{1}{t^2} $$
The simplified expression is ( \frac{1}{t^2} ).
More Information
When simplifying expressions with exponents, it's essential to remember that a negative exponent indicates a reciprocal. So, ( t^{-2} ) means one over ( t^2 ).
Tips
One common mistake is forgetting to apply the exponent rule correctly, especially with negative exponents. Ensure to combine the exponents accurately and recognize the meaning of negative exponents.
AI-generated content may contain errors. Please verify critical information