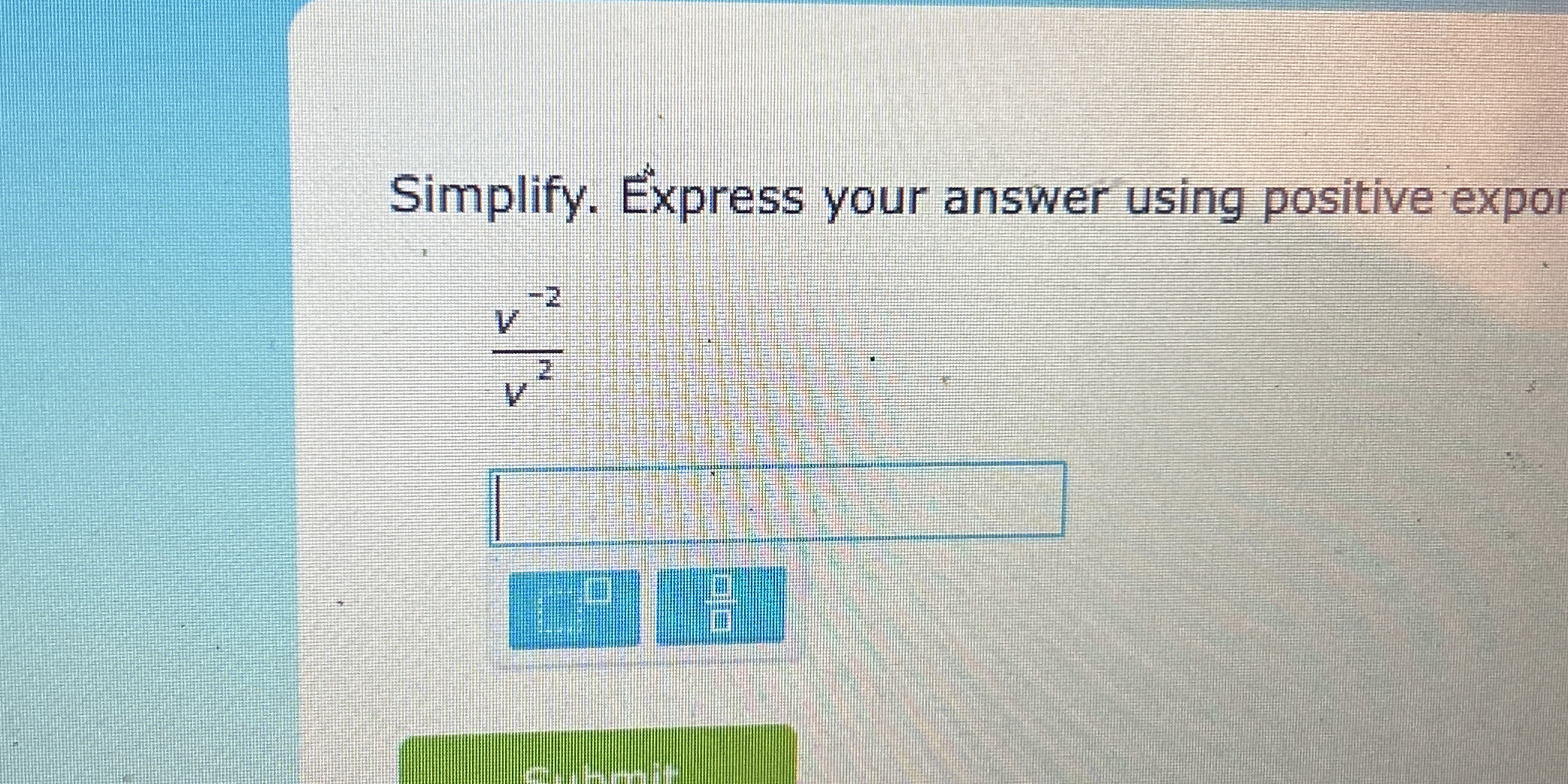
Simplify \( \frac{v^{-2}}{v^{-2}} \) and express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression ( \frac{v^{-2}}{v^{-2}} ) and express the answer using positive exponents. To solve this, we can apply the properties of exponents.
Answer
The simplified expression is \( 1 \).
Answer for screen readers
The simplified form of ( \frac{v^{-2}}{v^{-2}} ) is ( 1 ).
Steps to Solve
- Simplify the Fraction Start by simplifying the expression using the property of exponents:
$$ \frac{a^m}{a^n} = a^{m-n} $$
In this case, we have:
$$ \frac{v^{-2}}{v^{-2}} = v^{-2 - (-2)} = v^{0} $$
- Evaluate the Exponent Recall that any non-zero base raised to the power of zero equals one:
$$ v^{0} = 1 $$
Thus, the simplified form of the original expression is 1.
- Final Result The expression ( \frac{v^{-2}}{v^{-2}} ) was simplified to ( 1 ).
The simplified form of ( \frac{v^{-2}}{v^{-2}} ) is ( 1 ).
More Information
This result illustrates a fundamental property of exponents: any non-zero number raised to the power of zero equals one. This property is essential in algebra and mathematics in general.
Tips
- Overlooking the Zero Exponent Rule: Sometimes, students forget that any base (except zero) raised to the power of zero equals one. It’s vital to remember this when simplifying expressions.
AI-generated content may contain errors. Please verify critical information