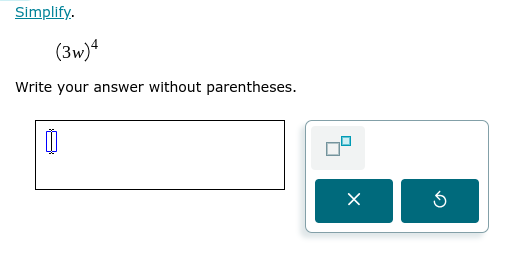
Simplify (3w)^4 and write your answer without parentheses.
Understand the Problem
The question is asking to simplify the expression (3w)^4. This involves applying the exponent to both the coefficient (3) and the variable (w) while also using the exponent rule which states that (a*b)^n = a^n * b^n.
Answer
$81w^4$
Answer for screen readers
The simplified expression is $81w^4$.
Steps to Solve
- Apply the exponent to each part of the expression
Use the exponent rule $(ab)^n = a^n \cdot b^n$. Here, $a$ is the coefficient (3) and $b$ is the variable (w).
- Simplify the coefficient
Raise the coefficient to the power of 4: $$ 3^4 = 3 \times 3 \times 3 \times 3 = 81 $$
- Simplify the variable
Raise the variable to the power of 4: $$ w^4 $$
- Combine the results
Combine the results from the previous steps: $$ (3w)^4 = 3^4 \cdot w^4 = 81w^4 $$
The simplified expression is $81w^4$.
More Information
This simplification shows how exponents work with both coefficients and variables. It’s an essential concept in algebra that helps in solving higher-level equations and expressions.
Tips
- Forgetting to apply the exponent to both the coefficient and the variable.
- Miscalculating the exponent, especially with larger numbers like $3^4$.
AI-generated content may contain errors. Please verify critical information