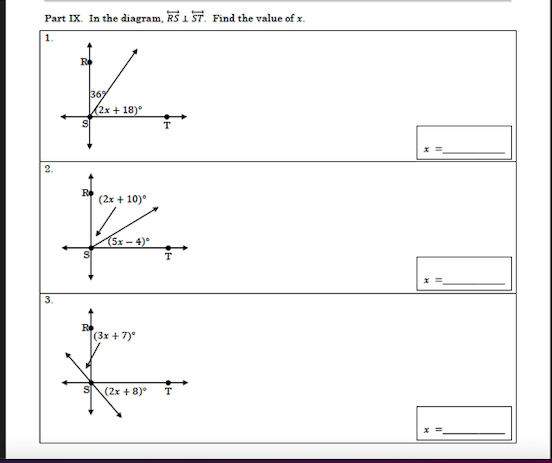
In the diagram, RS is perpendicular to ST. Find the value of x in the following statements: 1. 36° and (2x + 18)°. 2. (2x + 10)° and (5x - 4)°. 3. (3x + 7)° and (2x + 8)°.
Understand the Problem
The question is asking to find the value of x in a geometry problem involving angles, where certain angles are given in terms of x and are related through properties of intersecting lines (angles formed on a straight line).
Answer
1. $63$ 2. $24.857$ 3. $33$
Answer for screen readers
- $x = 63$
- $x \approx 24.857$
- $x = 33$
Steps to Solve
- Identify the relationships between angles
In each case, identify that the angles involve the property that angles on a straight line add up to $180^\circ$.
- Set up the equation for the first problem
For the first problem: $$ 36^\circ + (2x + 18)^\circ = 180^\circ $$
- Solve the equation for x
To solve for $x$, combine like terms: $$ 36 + 2x + 18 = 180 $$ This simplifies to: $$ 2x + 54 = 180 $$
Now, isolate $x$ by subtracting 54: $$ 2x = 180 - 54 $$ $$ 2x = 126 $$
Now divide by 2: $$ x = 63 $$
- Repeat for the second problem
Set up the equation: $$ (2x + 10)^\circ + (5x - 4)^\circ = 180^\circ $$
Combine like terms: $$ 2x + 10 + 5x - 4 = 180 $$ This simplifies to: $$ 7x + 6 = 180 $$
Isolate $x$: $$ 7x = 180 - 6 $$ $$ 7x = 174 $$ $$ x = 24.857 $$
- Repeat for the third problem
Set up the equation: $$ (3x + 7)^\circ + (2x + 8)^\circ = 180^\circ $$
Combine like terms: $$ 3x + 7 + 2x + 8 = 180 $$ This simplifies to: $$ 5x + 15 = 180 $$
Isolate $x$: $$ 5x = 180 - 15 $$ $$ 5x = 165 $$ $$ x = 33 $$
- $x = 63$
- $x \approx 24.857$
- $x = 33$
More Information
In these problems, we used the property that adjacent angles on a straight line are supplementary, meaning they add up to $180^\circ$.
Tips
- Forgetting to combine like terms correctly can lead to incorrect equations.
- Not applying the supplementary angles principle appropriately.
AI-generated content may contain errors. Please verify critical information