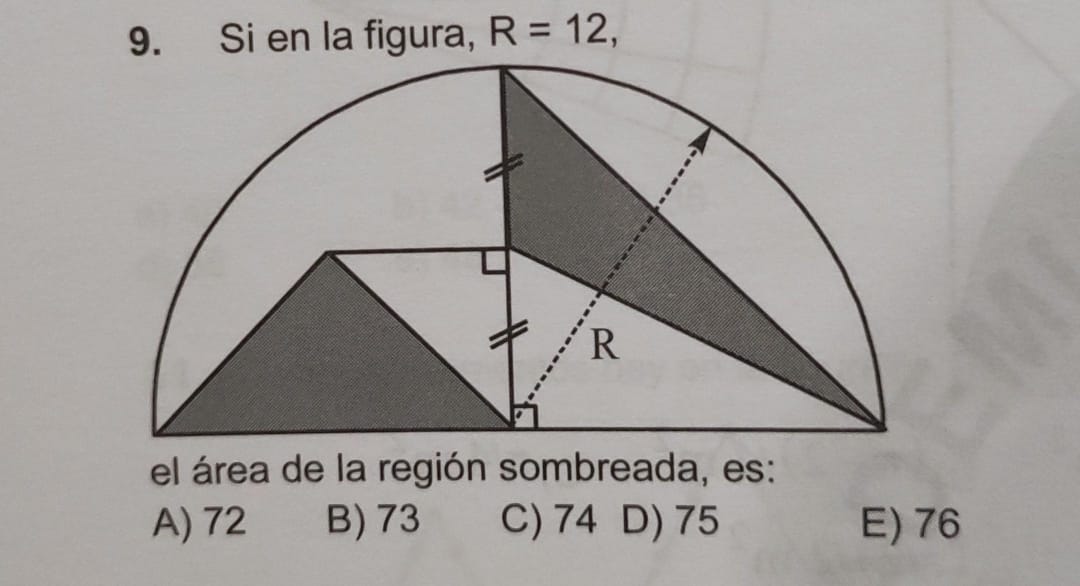
Si en la figura, R = 12, el área de la región sombreada, es:

Steps to Solve

1. Identificación de áreas de figuras

   La figura contiene un semicirculo y dos triángulos isósceles. Primero, calcularemos el área del semicirculo y luego las áreas de los triángulos.

2. Cálculo del área del semicirculo

   El área del semicirculo se calcula con la fórmula: $$ A_{\text{semicirculo}} = \frac{1}{2} \pi R^2 $$ Sustituyendo $R = 12$: $$ A_{\text{semicirculo}} = \frac{1}{2} \pi (12)^2 = \frac{1}{2} \pi \cdot 144 = 72\pi $$

3. Cálculo del área de un triángulo

   Cada triángulo tiene una base igual al radio del semicirculo, que es $12$, y una altura también de $12$. Usando la fórmula del área de un triángulo: $$ A_{\text{triángulo}} = \frac{1}{2} \cdot \text{base} \cdot \text{altura} $$ Sustituyendo los valores: $$ A_{\text{triángulo}} = \frac{1}{2} \cdot 12 \cdot 12 = 72 $$

4. Cálculo del área total de los triángulos

   Hay dos triángulos, por lo que multiplicamos el área de uno por dos: $$ A_{\text{total_triángulos}} = 2 \cdot A_{\text{triángulo}} = 2 \cdot 72 = 144 $$

5. Cálculo del área sombreada

   Para obtener el área de la región sombreada, restamos el área de los triángulos del área del semicirculo: $$ A_{\text{sombreada}} = A_{\text{semicirculo}} - A_{\text{total_triángulos}} $$ Entonces: $$ A_{\text{sombreada}} = 72\pi - 144 $$

6. Aproximación de $\pi$

   Aproximaremos $\pi \approx 3.14$ para calcular el área sombreada: $$ A_{\text{sombreada}} \approx 72(3.14) - 144 $$ $$ A_{\text{sombreada}} \approx 226.08 - 144 \approx 82.08 $$