Show that the area of R is given by the integral ∫(2, 0) (1 / ((t + 1)(t + 2))) dt.
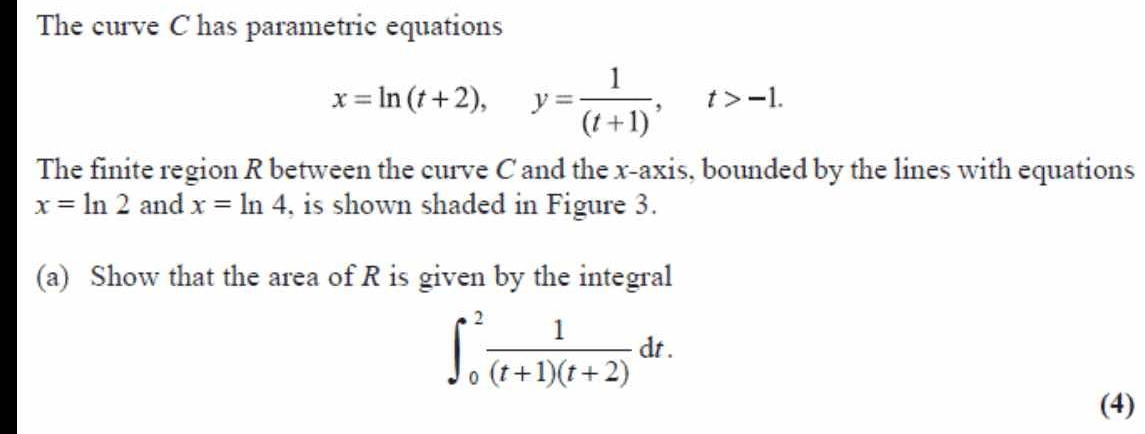
Understand the Problem
The question asks to demonstrate that the area of the region R, bounded by the given parametric equations and specific vertical lines, can be expressed as a definite integral. The goal is to show the relationship between the area and the provided integral formula.
Answer
The area \( R \) is given by the integral $$ \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} \, dt. $$
Answer for screen readers
The area ( R ) is given by the integral
$$ \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} , dt. $$
Steps to Solve
- Identify the area under the curve
The area ( A ) under the curve ( C ) from ( x = \ln 2 ) to ( x = \ln 4 ) can be expressed as:
$$ A = \int_{a}^{b} y , dx $$
where ( a = \ln 2 ) and ( b = \ln 4 ).
- Change of variables
Since the parametric equations are given by ( x = \ln(t + 2) ) and ( y = \frac{1}{t + 1} ), we first need to express ( y ) in terms of ( t ). We can relate ( t ) to ( x ) using the equation for ( x ):
$$ e^x = t + 2 \implies t = e^x - 2 $$
Substituting this into the equation for ( y ):
$$ y = \frac{1}{(e^x - 2) + 1} = \frac{1}{e^x - 1} $$
- Finding the derivative
Now we need to find ( \frac{dx}{dt} ) to convert the integral. We have ( x = \ln(t + 2) ):
$$ \frac{dx}{dt} = \frac{1}{t + 2} $$
Then, invert this to get ( dx ):
$$ dx = (t + 2) , dt $$
- Set the limits for ( t )
Now we need to establish the limits of integration in terms of ( t ). When ( x = \ln 2 ):
$$ 2 = t + 2 \implies t = 0 $$
When ( x = \ln 4 ):
$$ 4 = t + 2 \implies t = 2 $$
Thus, the new limits of integration are from ( t = 0 ) to ( t = 2 ).
- Substituting into the integral
The area ( A ) can now be expressed as:
$$ A = \int_{0}^{2} y \cdot \frac{dx}{dt} , dt $$
Substituting ( y = \frac{1}{t + 1} ) and ( \frac{dx}{dt} = (t + 2) ):
$$ A = \int_{0}^{2} \frac{1}{t + 1} \cdot (t + 2) , dt $$
- Final integral expression
This gives us:
$$ A = \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} , dt $$
Thus, we have shown that the area of region ( R ) is given by the integral:
$$ A = \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} , dt $$
The area ( R ) is given by the integral
$$ \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} , dt. $$
More Information
This integral represents the area under the curve defined by the parametric equations, bounded by the specified vertical lines. The function ( y = \frac{1}{t + 1} ) governs the height of the area between the curve and the x-axis.
Tips
- Forgetting to change the limits of integration when substituting from ( x ) to ( t ).
- Confusing ( y ) with ( t ); remember to substitute ( t ) correctly based on the parametric equations.
AI-generated content may contain errors. Please verify critical information