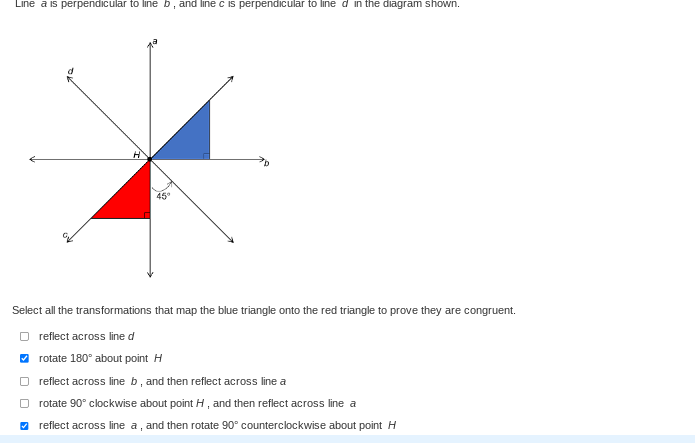
Select all the transformations that map the blue triangle onto the red triangle to prove they are congruent.
Understand the Problem
The question is asking which transformations can be applied to a blue triangle in a diagram in order to map it onto a red triangle, indicating that the two triangles are congruent. The user needs to evaluate various transformations including reflections and rotations.
Answer
- Rotate 180° about point $H$ - Rotate 90° clockwise about point $H$, then reflect across line $a$ - Reflect across line $a$, then rotate 90° counterclockwise about point $H$
Answer for screen readers
The transformations that map the blue triangle onto the red triangle are:
- Rotate 180° about point $H$
- Rotate 90° clockwise about point $H$, then reflect across line $a$
- Reflect across line $a$, then rotate 90° counterclockwise about point $H$
Steps to Solve
-
Identify the Transformations We will consider the various transformations that can map the blue triangle onto the red triangle. The transformations to evaluate include reflections and rotations.
-
Reflect Across Line d To reflect the blue triangle across line $d$, the triangle will switch positions while maintaining its orientation. This transformation alone will not map the blue triangle to the red triangle since their orientations will differ.
-
Rotate 180° about Point H Rotating the blue triangle 180° about point $H$ will position it directly over the red triangle because it will effectively flip the triangle over point $H$. This transformation successfully maps the blue triangle onto the red triangle.
-
Reflect Across Line b, then Reflect Across Line a First, reflecting the blue triangle across line $b$ will change its orientation. Reflecting it again across line $a$ will not return it to the original position in relation to the red triangle, thus it won't map correctly.
-
Rotate 90° Clockwise about Point H, then Reflect Across Line a Rotating the blue triangle 90° clockwise about point $H$ will change its orientation. Following this with a reflection across line $a$ will place it in the correct position, so this transformation can map the blue triangle to the red triangle.
-
Reflect Across Line a, then Rotate 90° Counterclockwise about Point H Reflecting the blue triangle across line $a$ will change its position, then rotating it 90° counterclockwise about point $H$ can potentially align it with the red triangle. This transformation also correctly maps the blue triangle to the red triangle.
The transformations that map the blue triangle onto the red triangle are:
- Rotate 180° about point $H$
- Rotate 90° clockwise about point $H$, then reflect across line $a$
- Reflect across line $a$, then rotate 90° counterclockwise about point $H$
More Information
The congruence of triangles can be proven through transformations such as rotations and reflections, demonstrating that two shapes are identical in size and shape, despite potentially differing orientations or positions.
Tips
- Confusing the order of transformations: The order in which reflections and rotations are applied can significantly impact the final orientation and position of the triangle.
- Assuming any reflection or rotation will suffice: Not every transformation will map the triangles congruently; each needs careful evaluation based on the initial positions and orientations.
AI-generated content may contain errors. Please verify critical information