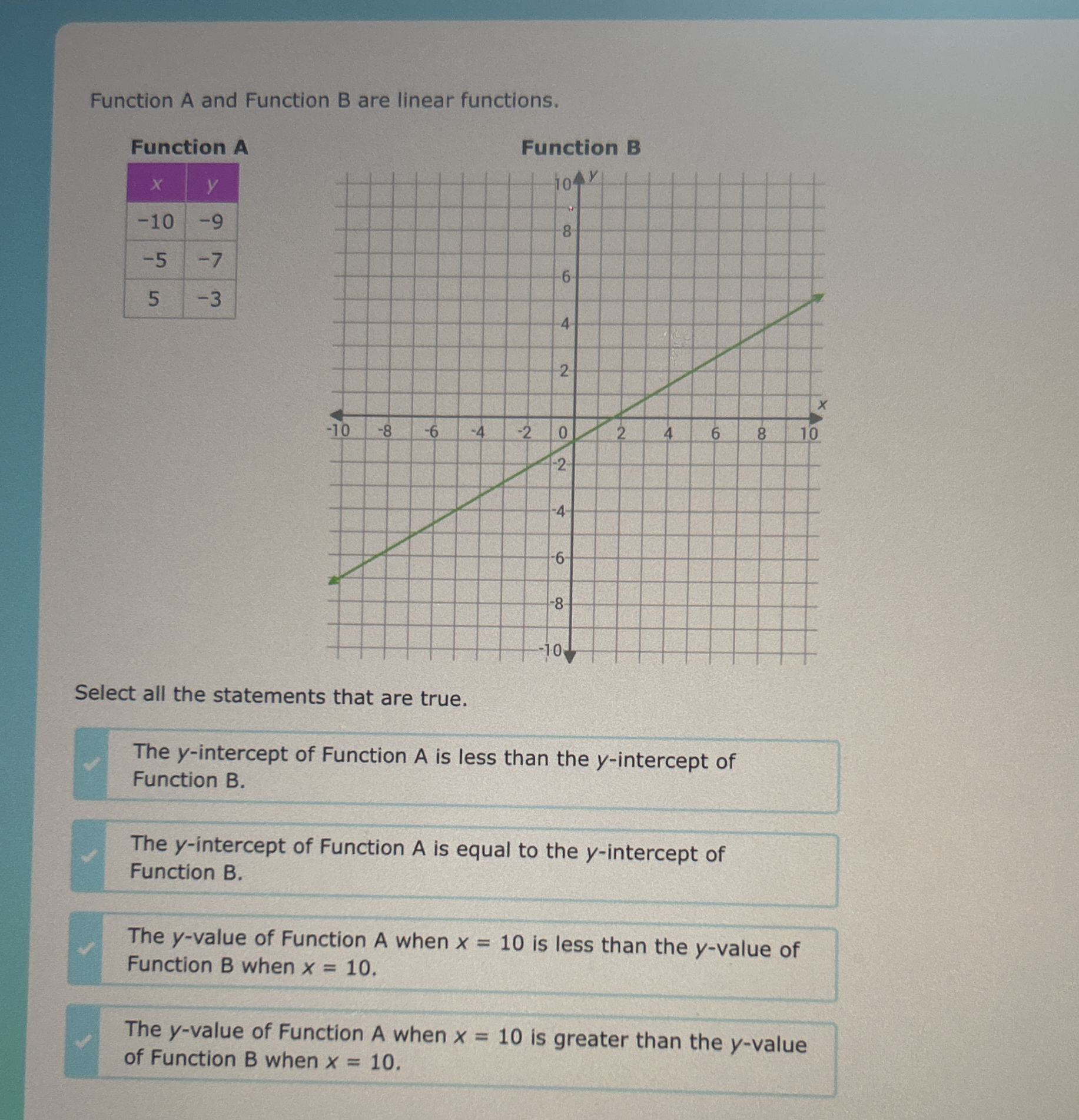
Select all the statements that are true about the functions A and B.

Steps to Solve

1. Determine the y-intercepts of Function A and Function B

To find the y-intercept, set $x = 0$ and solve for $y$ in each function.

For Function A, using the coordinates provided:

• When $x = -10$, $y = -9$

• When $x = -5$, $y = -7$

• When $x = 5$, $y = -3$

Using two points, we can find the slope $m$: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-7 - (-9)}{-5 - (-10)} = \frac{2}{5} $$

Now, using the point-slope form of the equation of a line to find the y-intercept: $$ y - y_1 = m(x - x_1) $$ Using the point (-10, -9): $$ y + 9 = \frac{2}{5}(x + 10) $$

Setting $x = 0$ gives: $$ y + 9 = 4 \Rightarrow y = -5 $$

Thus, the y-intercept of Function A is $-5$.

For Function B, we can determine the y-intercept directly from the graph, which appears to intersect the y-axis at $2$. So:

• The y-intercept of Function B is $2$.

2. Compare the y-intercepts

Now that we have both intercepts:

• Function A: $y = -5$
• Function B: $y = 2$

Since $-5 < 2$, the statement about y-intercepts of Function A being less than those of Function B is true.

3. Find the y-values when $x = 10$ for both functions

For Function A, calculate using the slope-intercept form. Given that $y = -5$, to find the corresponding function: Using the point-intercept form: $$ y = \frac{2}{5}x - 5 $$

Substituting $x = 10$: $$ y = \frac{2}{5}(10) - 5 = 4 - 5 = -1 $$

For Function B, observe that the graph at $x = 10$ suggests a higher value, based on the slope. By estimating, or using the points as the equation can be derived similarly to Function A.

However, since we see from the graph that it crosses around $y = 6$ when $x=10$, let’s confirm that visually. Thus:

• Function A at $x = 10$: $y_A = -1$
• Function B at $x = 10$: $y_B = 6$

4. Compare the y-values when $x = 10$

Comparatively, since $-1 < 6$, the corresponding statement is also true.

5. Verify the remaining statements

The remaining statements can now be analyzed:

• Function A $(-1)$ is not greater than Function B $(6)$.
• Function A is also not equal to Function B when $x = 10$.

Thus, the statements about equality and the greater relation are false.