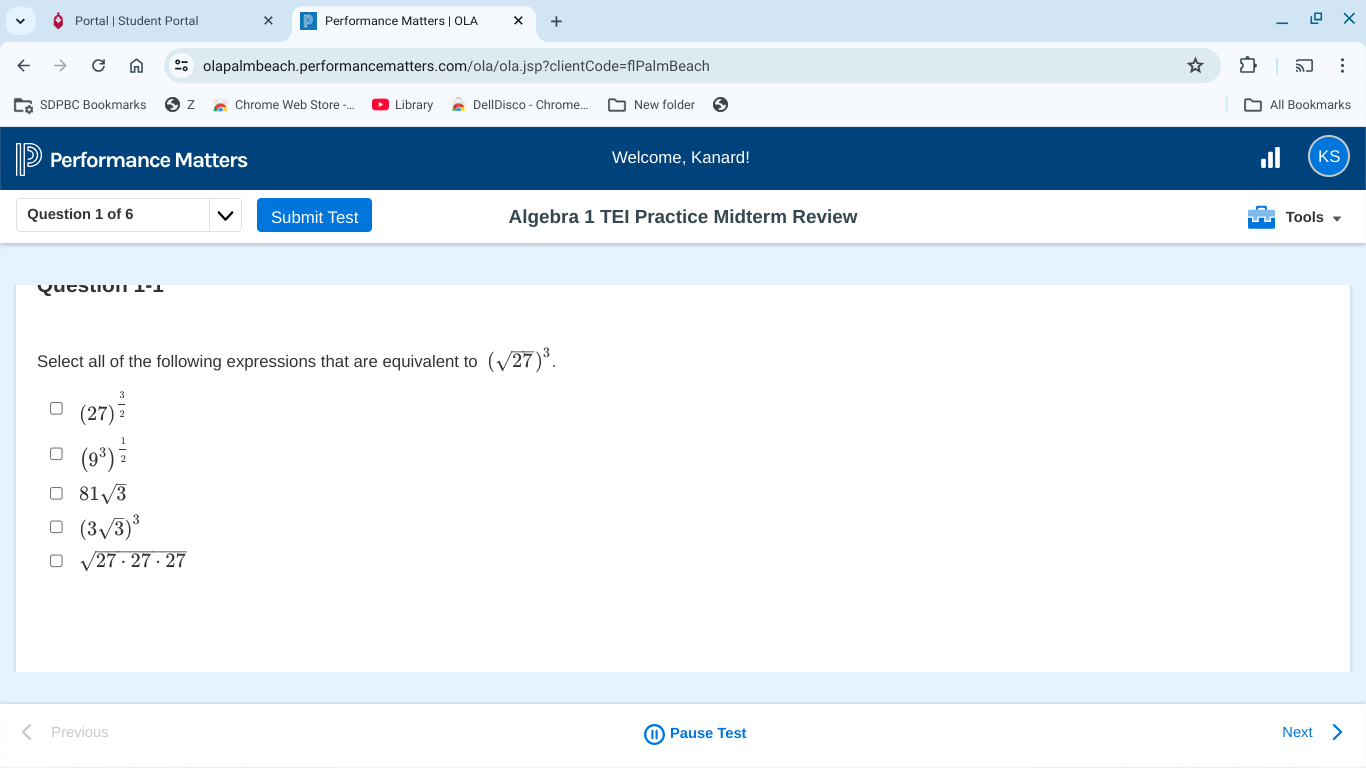
Select all of the following expressions that are equivalent to (√27)³.

Steps to Solve

1. Calculate the original expression

First, we need to simplify the expression $ (\sqrt{27})^3 $.

Knowing that $\sqrt{27} = 3\sqrt{3}$ (since $27 = 3^3$), we can rewrite the expression as: $$ (\sqrt{27})^3 = (3\sqrt{3})^3 $$

2. Use the properties of exponents

Using the property $(ab)^n = a^n \cdot b^n$, we can expand: $$ (3\sqrt{3})^3 = 3^3 \cdot (\sqrt{3})^3 $$

This simplifies to: $$ 3^3 \cdot 3^{3/2} $$

3. Combine the exponents

By adding the exponents (since the bases are the same): $$ 3^3 \cdot 3^{3/2} = 3^{3 + 3/2} = 3^{6/2 + 3/2} = 3^{9/2} $$

Thus, we have: $$ (\sqrt{27})^3 = 3^{9/2} $$

4. Evaluate the options

Now we need to evaluate each given expression to see if any simplify to $3^{9/2}$:

• First option: $ (27)^{\frac{3}{2}} = (3^3)^{\frac{3}{2}} = 3^{3 \cdot \frac{3}{2}} = 3^{\frac{9}{2}}$ (this is equivalent)

• Second option: $ (9^3)^{\frac{1}{2}} = 9^{\frac{3}{2}} = (3^2)^{\frac{3}{2}} = 3^{2 \cdot \frac{3}{2}} = 3^3$ (not equivalent)

• Third option: $ 81\sqrt{3} = 3^4 \cdot 3^{\frac{1}{2}} = 3^{4 + \frac{1}{2}} = 3^{\frac{9}{2}}$ (this is equivalent)

• Fourth option: $(3\sqrt{3})^3 = 3^{9/2}$ (this is equivalent)

• Fifth option: $ \sqrt{27 \cdot 27 \cdot 27} = \sqrt{27^3} = (27)^{3/2} = 3^{\frac{9}{2}}$ (this is equivalent)