Say true or false and justify. 10 x 10^11 = 1001 (i) 3° = 1000° (iv)
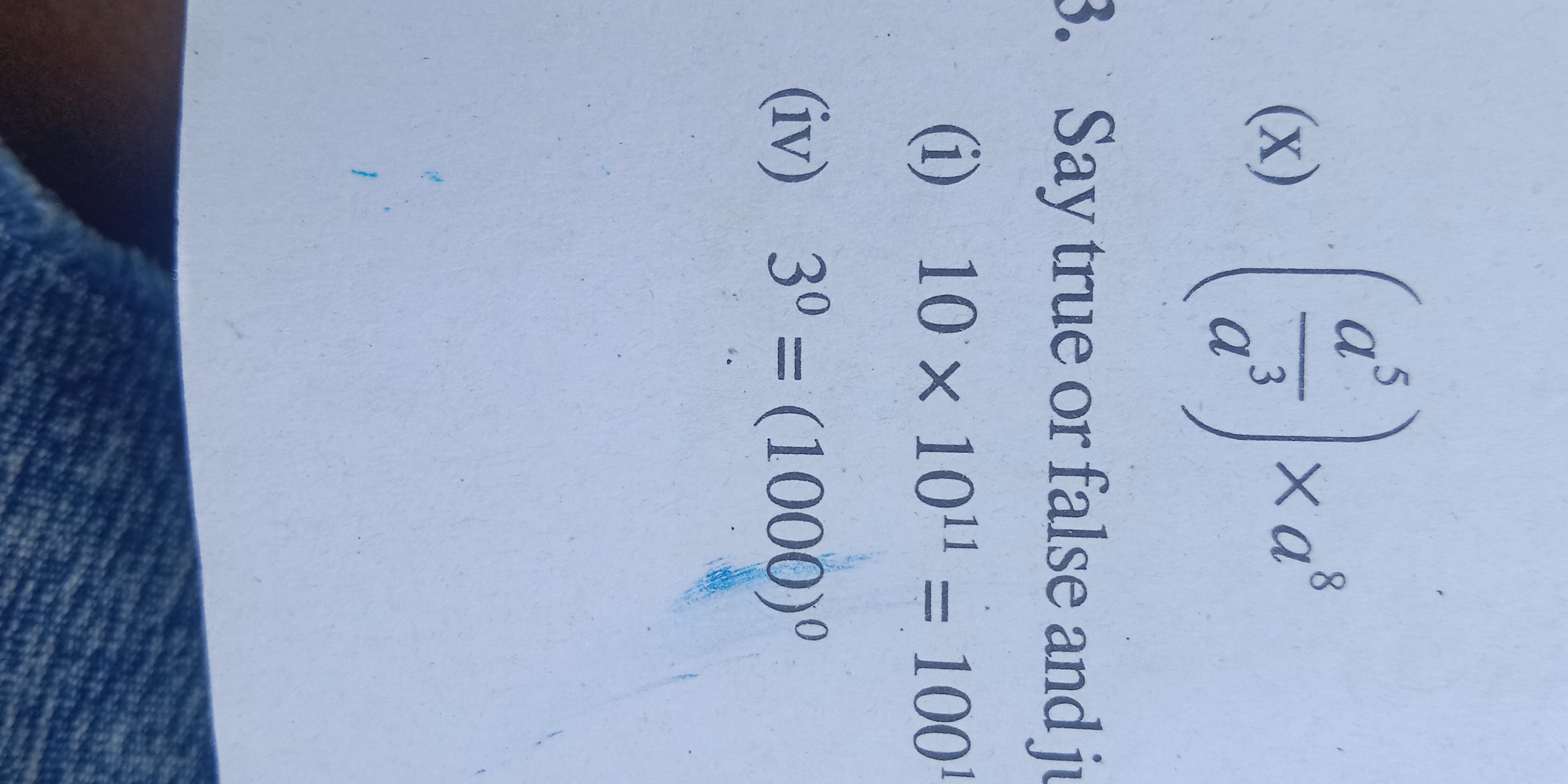
Understand the Problem
The question is asking us to determine whether the statements provided regarding mathematics (specifically, exponent and numerical operations) are true or false, and to justify our answers accordingly.
Answer
True, $3^0 = (1000)^0 = 1$.
Answer for screen readers
The answer is true, ( 3^0 = (1000)^0 ) evaluates to ( 1 = 1 ).
Steps to Solve
-
Understanding the Expression
The expression given is ( 3^0 = (1000)^0 ). According to the rules of exponents, any non-zero number raised to the power of zero is equal to 1. Therefore, we expect both sides of the equation to evaluate to the same value. -
Evaluate the Left Side
Calculate ( 3^0 ):
Since ( 3^0 = 1 ), the left side evaluates to 1. -
Evaluate the Right Side
Calculate ( (1000)^0 ):
According to the same rule of exponents, ( 1000^0 = 1 ). Thus, the right side also evaluates to 1. -
Compare Both Sides
Now we compare both sides of the equation:
Left Side: ( 1 )
Right Side: ( 1 )
Since both sides are equal, the statement is true.
The answer is true, ( 3^0 = (1000)^0 ) evaluates to ( 1 = 1 ).
More Information
This statement is a direct application of the exponent rule that states any non-zero number raised to the power of zero is equal to 1. This rule is fundamental in algebra and is often used in various mathematical contexts.
Tips
- Mistaking zero for one: A common mistake is assuming ( x^0 ) equals ( 0 ) instead of ( 1 ). Remember, ( x^0 = 1 ) for all ( x \neq 0 ).
AI-generated content may contain errors. Please verify critical information