Sabendo que f'(x) = x cos(x/4) e f(0) = 0, calcule f(π).
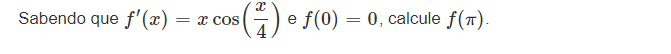
Understand the Problem
La pregunta está pidiendo calcular el valor de la función f(π) dado que su derivada es f'(x) = x cos(x/4) y el valor inicial f(0) = 0. Esto implica que debemos encontrar la función f(x) integrando f'(x) y aplicando la condición inicial.
Answer
$$ f(\pi) = 2\pi\sqrt{2} + 8\sqrt{2} - 16 $$
Answer for screen readers
$$ f(\pi) = 2\pi\sqrt{2} + 8\sqrt{2} - 16 $$
Steps to Solve
- Integrar la función derivada
Para encontrar $f(x)$ a partir de $f'(x)$, integramos la función. Entonces, calculamos: $$ f(x) = \int f'(x) , dx = \int x \cos\left(\frac{x}{4}\right) , dx $$
- Aplicar integración por partes
Usamos la integración por partes donde elegimos:
- $u = x$ y $dv = \cos\left(\frac{x}{4}\right)dx$
Calculamos $du$ y $v$:
- $du = dx$
- Para $v$, integramos $dv$: $$ v = 4\sin\left(\frac{x}{4}\right) $$
Entonces la fórmula de integración por partes es: $$ \int u , dv = uv - \int v , du $$
Sustituyendo: $$ f(x) = x \cdot 4 \sin\left(\frac{x}{4}\right) - \int 4 \sin\left(\frac{x}{4}\right) , dx $$
- Integrar la parte restante
Para la segunda integral, integramos: $$ \int 4 \sin\left(\frac{x}{4}\right) , dx = -16 \cos\left(\frac{x}{4}\right) $$
Sustituyendo de nuevo, obtenemos: $$ f(x) = 4x \sin\left(\frac{x}{4}\right) + 16 \cos\left(\frac{x}{4}\right) + C $$
- Usar la condición inicial
Aplicamos la condición inicial $f(0) = 0$: $$ f(0) = 4(0) \sin(0) + 16 \cos(0) + C = 0 $$
Esto implica que $C = -16$.
- Resultado final de la función
Por lo tanto, la función es: $$ f(x) = 4x \sin\left(\frac{x}{4}\right) + 16 \cos\left(\frac{x}{4}\right) - 16 $$
- Calcular $f(\pi)$
Finalmente, evaluamos la función en $x = \pi$: $$ f(\pi) = 4\pi \sin\left(\frac{\pi}{4}\right) + 16 \cos\left(\frac{\pi}{4}\right) - 16 $$
Sabemos que $\sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}$ y $\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}$.
Por lo tanto: $$ f(\pi) = 4\pi \cdot \frac{\sqrt{2}}{2} + 16 \cdot \frac{\sqrt{2}}{2} - 16 $$ $$ = 2\pi\sqrt{2} + 8\sqrt{2} - 16 $$
$$ f(\pi) = 2\pi\sqrt{2} + 8\sqrt{2} - 16 $$
More Information
El resultado $f(\pi)$ se obtiene al evaluar la integral de la función derivada y aplicar la condición inicial. La función resultante es una combinación de términos trigonométricos, que son comunes en problemas de cálculo.
Tips
- Olvidar aplicar correctamente la condición inicial al determinar la constante de integración $C$.
- No utilizar la técnica de integración por partes adecuadamente.
- Cometer errores al evaluar las funciones trigonométricas, como confundir los valores de $\sin$ y $\cos$ en puntos específicos.
AI-generated content may contain errors. Please verify critical information