Représenter les courbes de niveau et esquisser le graphe de la fonction de deux variables f(x, y) = |2x - y + 1|.
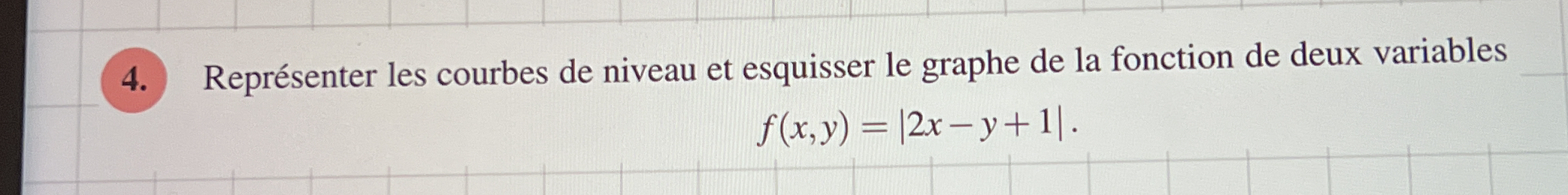
Understand the Problem
La question demande de représenter les courbes de niveau et d'esquisser le graphique d'une fonction de deux variables, donnée par f(x, y) = |2x - y + 1|.
Answer
Les courbes de niveau sont données par $y = 2x + 1 - k$ et $y = 2x + 1 + k$ pour différents $k$.
Answer for screen readers
Les courbes de niveau de la fonction $f(x, y) = |2x - y + 1|$ sont données par les équations des lignes $y = 2x + 1 - k$ et $y = 2x + 1 + k$ pour divers niveaux $k$.
Steps to Solve
-
Déterminer les courbes de niveau
Les courbes de niveau de la fonction $f(x, y) = |2x - y + 1|$ sont des lignes où $f(x, y) = k$, pour différents niveaux constants $k$.
Cela donne l'équation :
$$ |2x - y + 1| = k $$
Nous devons considérer deux cas :
- $2x - y + 1 = k$
- $2x - y + 1 = -k$
-
Résoudre pour $\mathbf{y}$ dans chaque cas
Pour le premier cas :
$$ 2x - y + 1 = k $$
Cela donne :
$$ y = 2x + 1 - k $$
Pour le second cas :
$$ 2x - y + 1 = -k $$
Cela donne :
$$ y = 2x + 1 + k $$
-
Tracer les lignes pour différents $k$
Nous allons tracer $y = 2x + 1 - k$ et $y = 2x + 1 + k$ pour plusieurs valeurs de $k$. Par exemple, pour $k = 0, 1, 2$, vous obtiendrez différentes lignes. -
Esquisser le graphe de la fonction
La fonction $f(x, y) = |2x - y + 1|$ existe dans le plan $3D$ et prend les valeurs de $y$ en fonction de $x$.
Pour un graphe simple, vous pouvez évaluer quelques points sur ces lignes et dessiner la surface correspondante au-dessus du plan.
Les courbes de niveau de la fonction $f(x, y) = |2x - y + 1|$ sont données par les équations des lignes $y = 2x + 1 - k$ et $y = 2x + 1 + k$ pour divers niveaux $k$.
More Information
Cette fonction représente la distance entre le plan défini par l'équation linéaire $2x - y + 1 = 0$ et l'origine (0,0) dans l'espace. Les courbes de niveau sont des lignes droites qui se déplacent à mesure que $k$ varie.
Tips
- Oublier de considérer le cas négatif lors de la manipulation de valeurs absolues.
- Ne pas tracer suffisamment de valeurs pour $k$, limitant ainsi la compréhension des courbes de niveau.
AI-generated content may contain errors. Please verify critical information