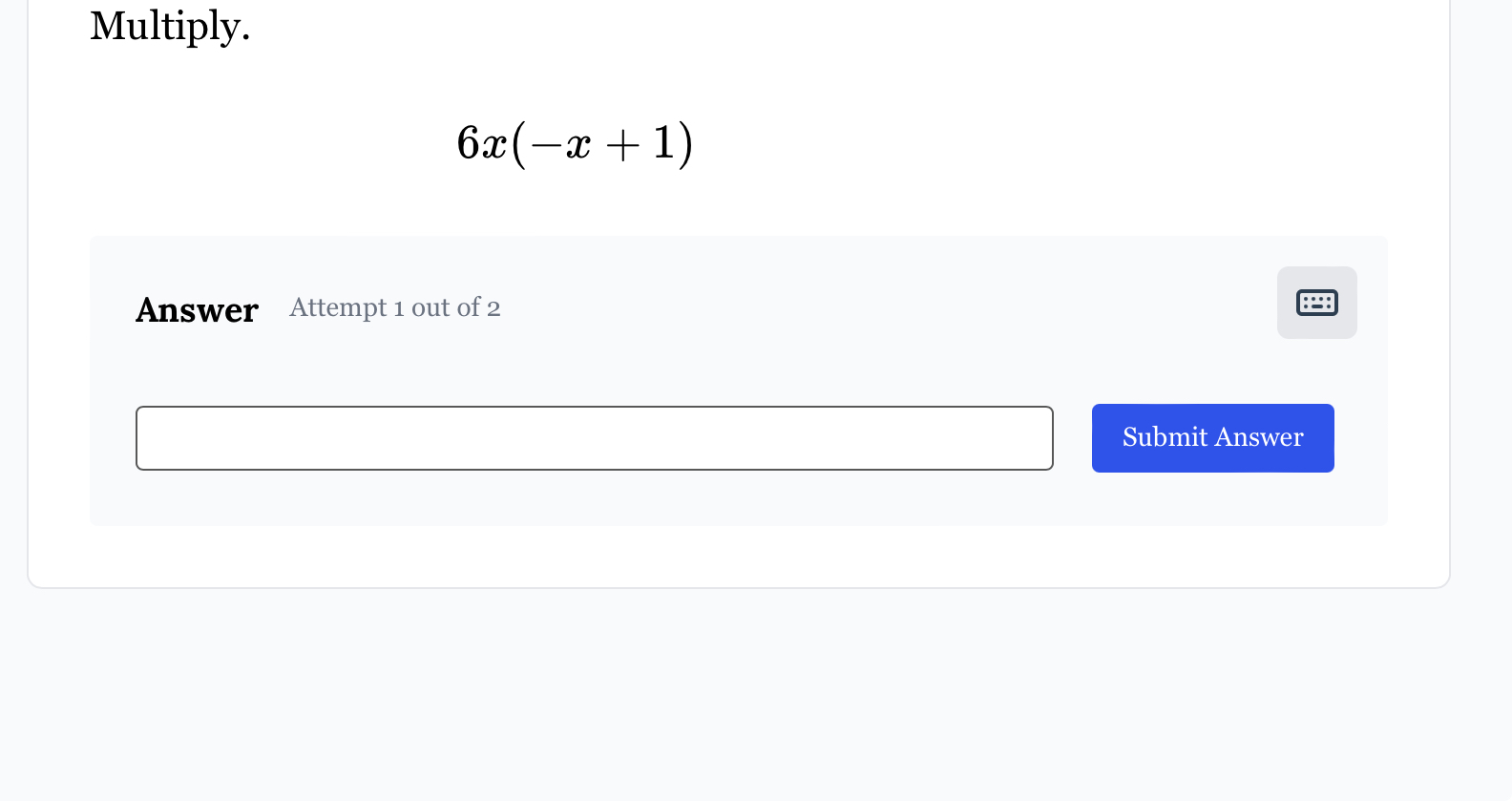
Multiply 6x(-x + 1).
Understand the Problem
The question is asking to multiply the expression 6x(-x + 1), which involves distributing the term 6x across the terms within the parentheses.
Answer
$$ -6x^2 + 6x $$
Answer for screen readers
The final answer is: $$ -6x^2 + 6x $$
Steps to Solve
- Distribute the first term To multiply the expression ( 6x(-x + 1) ), we distribute ( 6x ) to both terms inside the parentheses.
The first multiplication will be: $$ 6x \cdot (-x) $$
-
Calculate the first multiplication The result of the first multiplication is: $$ -6x^2 $$
-
Distribute ( 6x ) to the second term Next, we multiply ( 6x ) by the second term ( 1 ): $$ 6x \cdot 1 $$
-
Calculate the second multiplication The result of the second multiplication is: $$ 6x $$
-
Combine the results Now, we combine the results of the two multiplications: $$ -6x^2 + 6x $$
The final answer is: $$ -6x^2 + 6x $$
More Information
This expression represents a quadratic polynomial. The first term, ( -6x^2 ), indicates it opens downwards because of the negative coefficient, while the second term ( 6x ) contributes to the linear component of the polynomial.
Tips
- Forgetting to distribute to both terms inside the parentheses.
- Mixing up signs during multiplication (especially when multiplying by negative numbers).
AI-generated content may contain errors. Please verify critical information