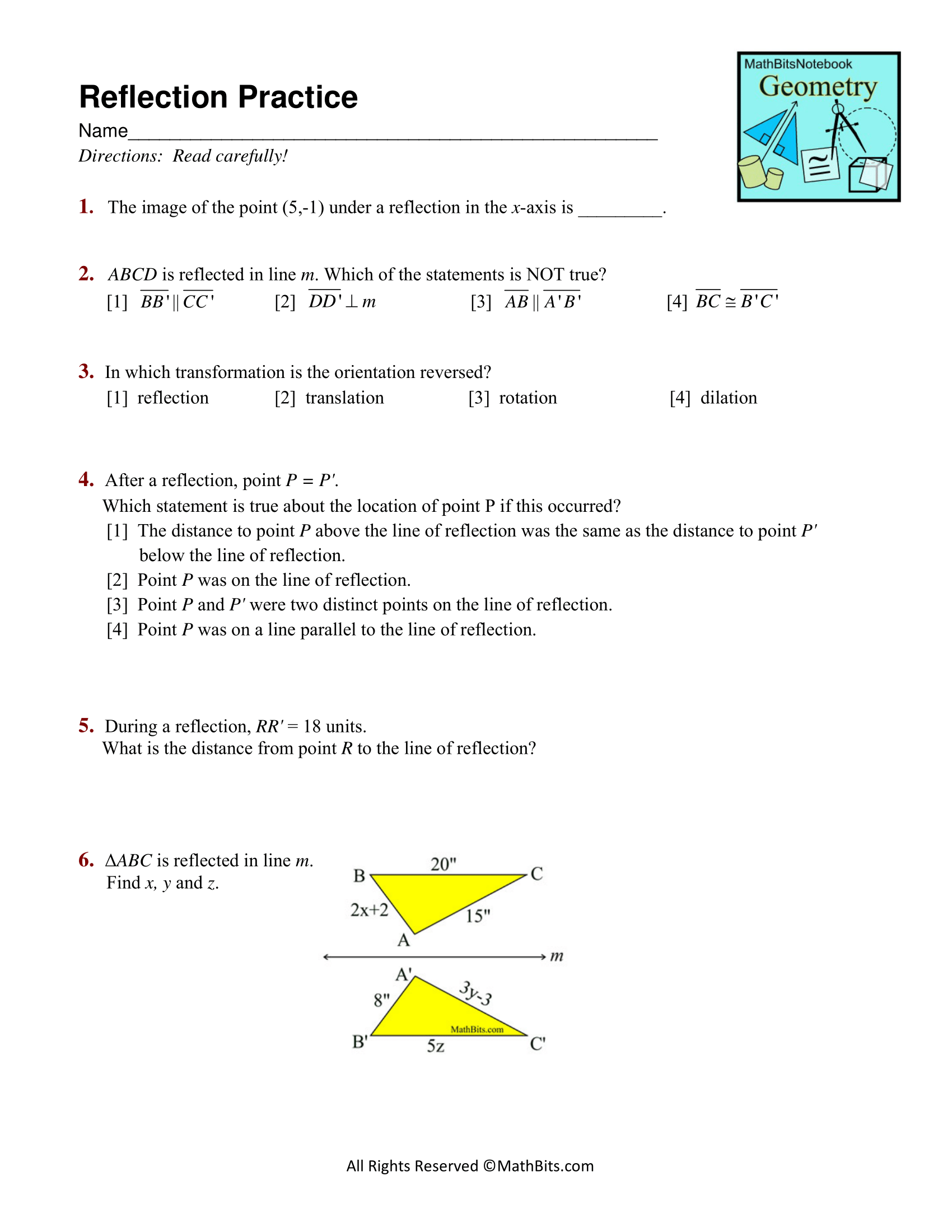
Reflection Practice. 1. The image of the point (5,-1) under a reflection in the x-axis is ________. 2. ABCD is reflected in line m. Which of the statements is NOT true? 3. In which... Reflection Practice. 1. The image of the point (5,-1) under a reflection in the x-axis is ________. 2. ABCD is reflected in line m. Which of the statements is NOT true? 3. In which transformation is the orientation reversed? 4. After a reflection, point P = P'. Which statement is true about the location of point P if this occurred? 5. During a reflection, RR' = 18 units. What is the distance from point R to the line of reflection? 6. ΔABC is reflected in line m. Find x, y and z.
Understand the Problem
The question pertains to geometry, specifically reflections and transformations. It asks various questions related to reflections, including point images, properties of figures after reflection, distances, and the relationship between points and lines during transformation.
Answer
1. $(5, 1)$ 2. [4] 3. Reflection 4. [1] 5. 9 units 6. \(x = 9\), \(y = \frac{11}{3}\), \(z = 3\)
Answer for screen readers
-
The image of the point $(5, -1)$ under a reflection in the x-axis is $(5, 1)$.
-
Statement [4] is NOT true about the reflection properties.
-
The transformation that reverses orientation is reflection.
-
The correct statement about point P is: [1].
-
The distance from point R to the line of reflection is (9) units.
-
The solved values are (x = 9), (y = \frac{11}{3}), and (z = 3).
Steps to Solve
- Reflecting a Point in the x-axis
To find the image of the point $(5, -1)$ under reflection in the x-axis, the y-coordinate changes sign.
Thus, the image is: $$ (5, -(-1)) = (5, 1) $$
- Identifying the False Statement About Reflection
For the reflection of quadrilateral ABCD in line m, we need to determine which statement is NOT true. This involves understanding the properties of reflections:
- Statement [1]: True, as segments reflected over a line are parallel.
- Statement [2]: True, as the distance between reflections maintains perpendicularity.
- Statement [3]: True, as corresponding segments are indeed parallel after transformation.
- Statement [4]: False, if it contradicts another property of reflection.
Inspect statements closely to find the false statement.
- Understanding Orientation Reversal
In identifying which transformation reverses orientation:
- Reflection reverses orientation (true).
- Translation does not reverse orientation (false).
- Rotation does not reverse orientation (false).
- Dilation does not alter position (false).
Thus, the answer is reflection.
- Analyzing Reflection of Point P
When reflecting point P to point P':
- The distance condition must hold: Statement [1]: True, as distance above and below remain equal. Statement [2]: True, as point P would be fixed at the line. Statement [3]: True if two distinct points are used. Statement [4]: False, if point P is actually on the line.
Identify the true statement by analyzing conditions.
- Distance Calculation in Reflection
Given the reflection condition ( RR' = 18 ) units, the distance from point R to the line of reflection can be derived from the relationship of points and their images. If the distance is half of 18 since it’s symmetrical: $$ \text{Distance from R to line} = \frac{18}{2} = 9 \text{ units} $$
- Solving for x, y, z in Triangle ABC
From reflection properties in triangle ABC:
- Set equations based on the given segment lengths and solve:
- From $2x + 2 = 20$, solve for $x$.
- From $3y - 3 = 8$, solve for $y$.
- From $5z = 15$, solve for $z$.
Solve the equations step by step to find x, y, and z values.
-
The image of the point $(5, -1)$ under a reflection in the x-axis is $(5, 1)$.
-
Statement [4] is NOT true about the reflection properties.
-
The transformation that reverses orientation is reflection.
-
The correct statement about point P is: [1].
-
The distance from point R to the line of reflection is (9) units.
-
The solved values are (x = 9), (y = \frac{11}{3}), and (z = 3).
More Information
Reflections maintain the distances and angles but reverse the orientation of shapes. The distance from a point to a line during reflection is critical for symmetry.
Tips
- Not changing the sign of the y-coordinate when reflecting across the x-axis.
- Misunderstanding which statements are true regarding properties of reflections.
- Not correctly solving algebraic equations for x, y, and z.
AI-generated content may contain errors. Please verify critical information