P(x) = x^4 - 4x^3 - 7x^2 + 22x + 24. Find P(-1).
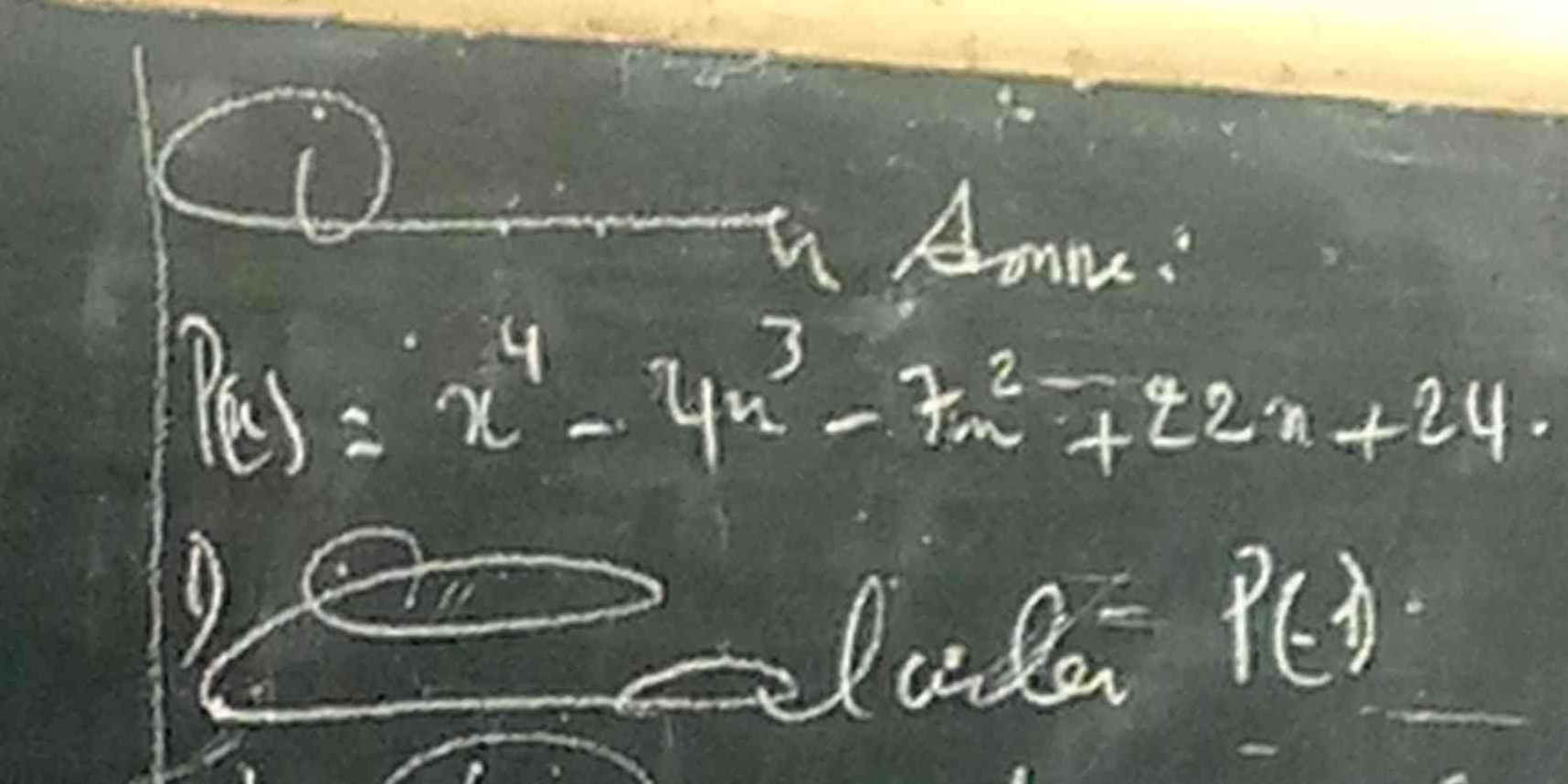
Understand the Problem
The question is presenting a polynomial function P(x) and seems to be asking for evaluation at a certain point, specifically P(-1). This involves substituting -1 into the function and calculating the result.
Answer
The value of $P(-1)$ is $0$.
Answer for screen readers
The value of $P(-1)$ is $0$.
Steps to Solve
-
Substitute -1 into the polynomial To find $P(-1)$, substitute $x = -1$ into the polynomial function $P(x) = x^4 - 4x^3 - 7x^2 + 22x + 24$. $$ P(-1) = (-1)^4 - 4(-1)^3 - 7(-1)^2 + 22(-1) + 24 $$
-
Calculate each term step by step Evaluate each term separately:
- First term: $(-1)^4 = 1$
- Second term: $-4(-1)^3 = -4(-1) = 4$
- Third term: $-7(-1)^2 = -7(1) = -7$
- Fourth term: $22(-1) = -22$
- Fifth term: $24$
Putting it all together: $$ P(-1) = 1 + 4 - 7 - 22 + 24 $$
-
Combine the results Now, add and subtract the values calculated: $$ P(-1) = (1 + 4) + 24 - (7 + 22) $$ $$ P(-1) = 5 + 24 - 29 $$
-
Final calculation Simplify the equation: $$ P(-1) = 29 - 29 = 0 $$
The value of $P(-1)$ is $0$.
More Information
The output $0$ indicates that $-1$ is a root of the polynomial $P(x)$. This means that when graphing the polynomial, the curve intersects the x-axis at $x = -1$.
Tips
Null
AI-generated content may contain errors. Please verify critical information