The system of linear equations in x1, x2, x3 where α, β ∈ R has at least one solution for any α and β.
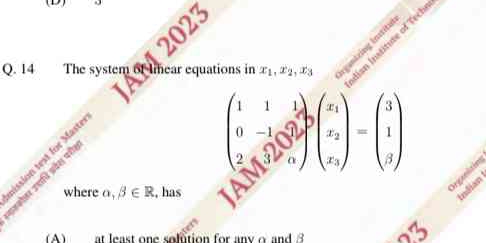
Understand the Problem
The question is asking us to analyze a system of linear equations and determine under what conditions (for values of α and β) there is at least one solution for the system. This involves concepts of linear algebra, specifically the conditions for the existence of solutions to a system of linear equations.
Answer
The system has at least one solution for any \( \alpha \) if \( \beta \neq 0 \).
Answer for screen readers
The system has at least one solution for any ( \alpha ) if ( \beta \neq 0 ).
Steps to Solve
- Write the system of equations
The given system of linear equations can be expressed in matrix form as follows:
$$ \begin{pmatrix} 1 & 1 & 0 \ 0 & -1 & 2 \ \alpha & 0 & \beta \end{pmatrix} \begin{pmatrix} x_1 \ x_2 \ x_3 \end{pmatrix}
\begin{pmatrix} 3 \ 1 \ \beta \end{pmatrix} $$
- Analyze the coefficient matrix
To determine the conditions under which the system has at least one solution, we need to check the coefficient matrix ( A ):
$$ A = \begin{pmatrix} 1 & 1 & 0 \ 0 & -1 & 2 \ \alpha & 0 & \beta \end{pmatrix} $$
- Determine the determinant of the coefficient matrix
For the system to have at least one solution for any values of ( \alpha ) and ( \beta ), the determinant of the coefficient matrix must not be zero (i.e., we cannot have an inconsistent system):
To find the determinant, compute ( \text{det}(A) ):
$$ \text{det}(A) = 1(-1 \cdot \beta - 0 \cdot 2) - 1(0 \cdot \beta - 0 \cdot \alpha) + 0(0 \cdot 2 - \alpha \cdot -1) = -\beta $$
- Set the determinant condition
For the matrix to be invertible and have at least one solution, we set the determinant condition:
$$ -\beta \neq 0 \implies \beta \neq 0 $$
This shows that for any ( \alpha ), if ( \beta = 0 ), the system may not have a solution.
- Conclusion of conditions
Therefore, for the system to have at least one solution for every ( \alpha ), we conclude:
- If ( \beta \neq 0 ), there is at least one solution.
- If ( \beta = 0 ), we must check the equations for consistency.
The system has at least one solution for any ( \alpha ) if ( \beta \neq 0 ).
More Information
In a system of linear equations, the existence of a solution often depends on the properties of the coefficient matrix. A system is consistent (it has at least one solution) when the determinant of the coefficient matrix is non-zero.
Tips
- Forgetting to check the determinant condition.
- Assuming that a solution exists for all values of ( \alpha ) and ( \beta ) without considering the case where ( \beta = 0 ).
AI-generated content may contain errors. Please verify critical information