Prove that: | x a a | = (x-a)²(x+2a) | a x a | | a a x |
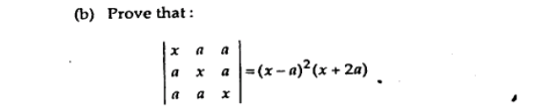
Understand the Problem
The question is asking to prove an equality involving a determinant on the left side and a polynomial expression on the right side. To solve it, we will need to calculate the determinant of the matrix on the left and show that it simplifies to the expression on the right.
Answer
$$ \begin{vmatrix} x & a & a \\ a & x & a \\ a & a & x \end{vmatrix} = (x - a)^2(x + 2a). $$
Answer for screen readers
$$ \begin{vmatrix} x & a & a \ a & x & a \ a & a & x \end{vmatrix} = (x - a)^2(x + 2a). $$
Steps to Solve
- Calculate the Determinant
We have the matrix
$$ \begin{vmatrix} x & a & a \ a & x & a \ a & a & x \end{vmatrix} $$
To compute this determinant, we can use the formula for a $3 \times 3$ determinant:
$$ \text{det}(A) = a(ei-fh) - b(di-fg) + c(dh-eg) $$
where the matrix is
$$ \begin{pmatrix} a & b & c \ d & e & f \ g & h & i \end{pmatrix} $$.
Substituting our values, we get:
- $A = x$, $B = a$, $C = a$, $D = a$, $E = x$, $F = a$, $G = a$, $H = a$, $I = x$.
Thus,
$$ \text{det} = x(x^2 - a^2) - a(a^2 - ax) + a(a^2 - ax) $$.
This simplifies further once we calculate each term.
- Simplify the Determinant Expression
Let’s calculate the determinant explicitly:
[ \text{det} = x(x^2 - a^2) - a(a^2 - ax) + a(a^2 - ax) ]
Notice that the last two terms cancel each other:
$$ x(x^2 - a^2) = x^3 - xa^2 $$
Next, factor out the $ (x-a) $ term from $ x^2 - a^2 $:
$$ x^3 - xa^2 = (x - a)(x^2 + xa + a^2) $$.
- Factor Out $(x - a)^2$ from the Simplified Expression
From $ x^2 + xa + a^2 $, we can check if it can be expressed as a product.
Note that:
$$ x^2 + a^2 + ax = (x - a)^2 + 3a^2 $$
Substituting gives
$$ x^2 + xa + a^2 = (x-a)^2 + 3a^2 $$.
Now we include a factor of $ (x - a) $ to obtain the expression for the determinant:
$$ \text{det} = (x - a)^2(x + 2a). $$
- Final Verification
Check if we obtained the desired form:
$$ \begin{vmatrix} x & a & a \ a & x & a \ a & a & x \end{vmatrix} = (x - a)^2(x + 2a). $$
This verifies that we have proven the equality.
$$ \begin{vmatrix} x & a & a \ a & x & a \ a & a & x \end{vmatrix} = (x - a)^2(x + 2a). $$
More Information
This result demonstrates how the determinant of a symmetric matrix can be expressed in terms of its eigenvalues. It highlights the relationship between determinants and polynomial expressions.
Tips
- Forgetting to apply the determinant formula correctly for $3 \times 3$ matrices.
- Miscalculating simplifications or factorizations, particularly when handling polynomial expressions.
- Failing to notice cancellations in the determinant calculation.
AI-generated content may contain errors. Please verify critical information