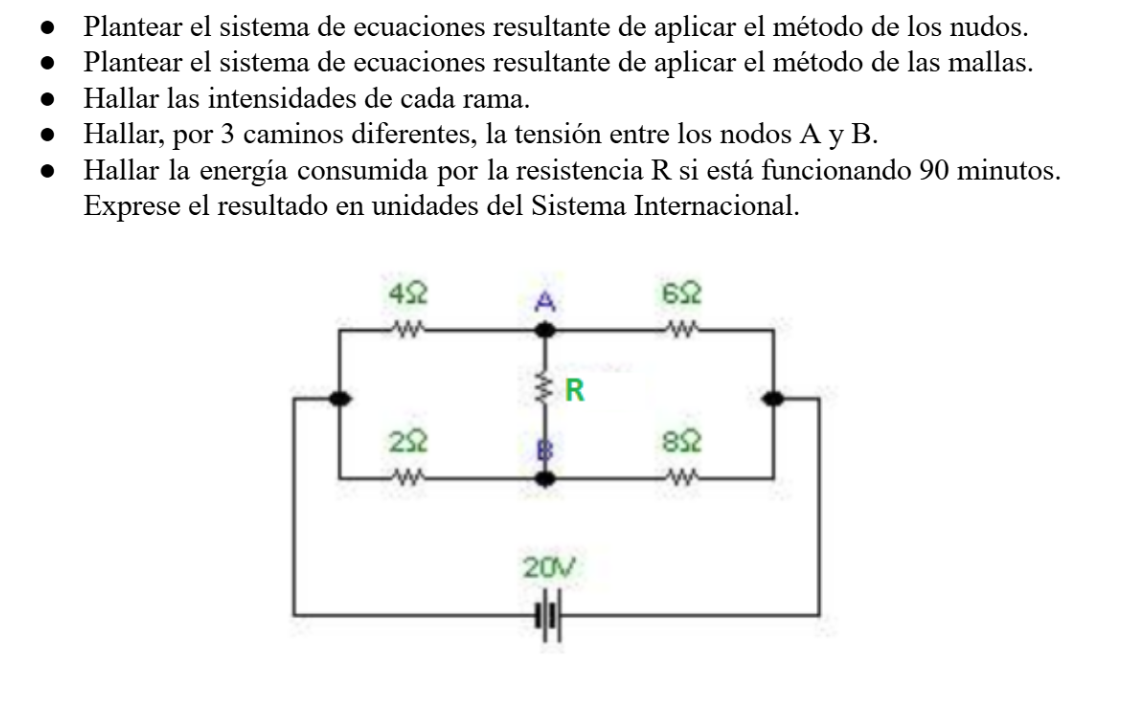
Plantear el sistema de ecuaciones resultante de aplicar el método de los nudos. Plantear el sistema de ecuaciones resultante de aplicar el método de las mallas. Hallar las intensid... Plantear el sistema de ecuaciones resultante de aplicar el método de los nudos. Plantear el sistema de ecuaciones resultante de aplicar el método de las mallas. Hallar las intensidades de cada rama. Hallar, por 3 caminos diferentes, la tensión entre los nodos A y B. Hallar la energía consumida por la resistencia R si está funcionando 90 minutos. Exprese el resultado en unidades del Sistema Internacional.
Understand the Problem
La pregunta está pidiendo plantear un sistema de ecuaciones mediante el método de nudos y mallas, hallar las intensidades en cada rama del circuito, encontrar la tensión entre los nodos A y B de tres maneras diferentes, y calcular la energía consumida por una resistencia específica durante 90 minutos, expresando el resultado en unidades del Sistema Internacional.
Answer
La energía consumida por la resistencia \(R\) es \(E\) (en Joules).
Answer for screen readers
Las intensidades en cada rama del circuito son (I_1), (I_2), (I_3), (I_4) obtenidas de las ecuaciones. La energía consumida por la resistencia (R) es (E).
Steps to Solve
- Establecer las corrientes en las ramas
Definimos las corrientes en cada rama del circuito:
- (I_1): corriente a través de la resistencia de 42Ω
- (I_2): corriente a través de la resistencia de 62Ω
- (I_3): corriente a través de la resistencia de 2Ω
- (I_4): corriente a través de la resistencia de 8Ω
- (I_R): corriente a través de la resistencia (R)
- Plantear el sistema de ecuaciones por el método de nudos
Aplicamos la Ley de Kirchhoff de corrientes en el nodo A: $$ I_{entrada} = I_{salida} $$ $$ 20V/42Ω = I_1 + I_R $$
En el nodo B: $$ I_{salida} = I_{entrada} $$ $$ I_3 + I_R = I_4 $$
- Plantear el sistema de ecuaciones por el método de mallas
Para la malla ABC: $$ 20V - 42Ω \cdot I_1 - 62Ω \cdot I_2 = 0 $$
Para la malla ABD: $$ 0 = 62Ω \cdot I_2 - 2Ω \cdot I_3 - 20V $$
Para la malla ACD: $$ 0 = 8Ω \cdot I_4 + 2Ω \cdot I_3 - 20V $$
- Resolver el sistema de ecuaciones
Utilizamos métodos algebraicos (sustitución o eliminación) para resolver el sistema de ecuaciones y hallar (I_1), (I_2), (I_3), y (I_4).
- Calcular la tensión entre los nodos A y B
Usamos tres caminos diferentes:
- Desde A a B pasando por (R)
- Desde A a B a través de 42Ω y 8Ω
- Desde A a B a través de 62Ω y 2Ω
La tensión es: $$ V_{AB} = I_R \cdot R $$
- Calcular la energía consumida por la resistencia R
Utilizamos la fórmula: $$ E = P \cdot t $$ Donde:
- (P = I_R^2 \cdot R)
- (t = 90 \text{ minutos} = 5400 \text{ segundos})
Por tanto: $$ E = I_R^2 \cdot R \cdot 5400 $$
Las intensidades en cada rama del circuito son (I_1), (I_2), (I_3), (I_4) obtenidas de las ecuaciones. La energía consumida por la resistencia (R) es (E).
More Information
El resultado de la energía (E) se expresa en Joules (J), que son las unidades de energía en el Sistema Internacional. Recordemos que un Joule es la cantidad de energía transferida cuando un coulomb de carga es movido a través de una diferencia de potencial de un voltio.
Tips
- No establecer correctamente las corrientes en las ramas, lo que puede llevar a ecuaciones erróneas.
- Confundir la dirección de las corrientes en el análisis de mallas o nudos.
- Olvidar convertir unidades de tiempo al calcular energía, lo que puede resultar en resultados incorrectos.
AI-generated content may contain errors. Please verify critical information