Steps to Solve

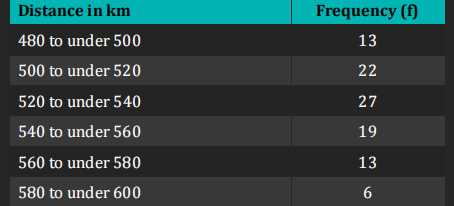
1. Calculate the Midpoint for Each Class To find the average for this frequency distribution, we first need to calculate the midpoint for each distance range. The midpoint can be found using the formula: $$ \text{Midpoint} = \frac{\text{Lower Limit} + \text{Upper Limit}}{2} $$ For example, for the distance range "480 to under 500": $$ \text{Midpoint} = \frac{480 + 500}{2} = 490 $$

2. List Each Midpoint and Corresponding Frequency Calculate the midpoints for all ranges:

• 480 to under 500: Midpoint = 490
• 500 to under 520: Midpoint = 510
• 520 to under 540: Midpoint = 530
• 540 to under 560: Midpoint = 550
• 560 to under 580: Midpoint = 570
• 580 to under 600: Midpoint = 590

3. Multiply Each Midpoint by its Frequency For each range, multiply the midpoint by the frequency:

• For 490: $490 \times 13 = 6370$
• For 510: $510 \times 22 = 11220$
• For 530: $530 \times 27 = 14310$
• For 550: $550 \times 19 = 10450$
• For 570: $570 \times 13 = 7410$
• For 590: $590 \times 6 = 3540$

4. Sum All the Products Add all the products obtained from the previous step: $$ 6370 + 11220 + 14310 + 10450 + 7410 + 3540 = 42000 $$

5. Calculate the Total Frequency Sum all the frequencies: $$ 13 + 22 + 27 + 19 + 13 + 6 = 100 $$

6. Calculate the Mean Distance Finally, divide the sum of the products by the total frequency to find the mean distance: $$ \text{Mean} = \frac{42000}{100} = 420 $$