p ∨ ¬(p ∧ q) (p → q) ↔ (¬p → ¬q) (p ∨ q) → ¬r ((a ∨ b) ∧ (a → c) ∧ (b → c)) → c
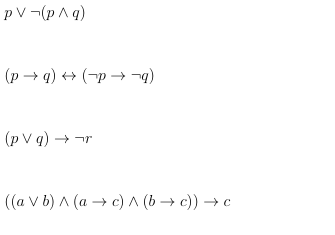
Understand the Problem
The question contains logical expressions and seeks to analyze or simplify them. It likely asks for truth values, validity, or implications of the given statements.
Answer
- The truth of the expressions varies; some are always true, others depend on specific variables.
Answer for screen readers
The answer involves evaluating each expression individually. The simplified form of each expression is as follows:
- For $p ∨ ¬(p ∧ q)$, the truth depends on $q$.
- $(p → q) ↔ (¬p → ¬q)$ is always true.
- $(p ∨ q) → ¬r$ depends on the values of $p$, $q$, and $r$.
- The last expression is logically valid.
Steps to Solve
- Analyze the first expression: $p ∨ ¬(p ∧ q)$
Using De Morgan's Laws, we can simplify the expression: $$ ¬(p ∧ q) = ¬p ∩ ¬q $$ Thus, the expression becomes: $$ p ∨ (¬p ∨ ¬q) = (p ∨ ¬p) ∨ ¬q $$
Since $p ∨ ¬p$ is always true (T), the entire expression simplifies to: $$ T ∨ ¬q $$
The truth value depends on $q$.
- Analyze the second expression: $(p → q) ↔ (¬p → ¬q)$
This is the contrapositive law, which states that a conditional statement is equivalent to its contrapositive. Therefore: $$ (p → q) ↔ (¬p → ¬q) \text{ is always true.} $$
- Analyze the third expression: $(p ∨ q) → ¬r$
This implies that if either $p$ or $q$ is true, $r$ must be false. The truth value of this expression depends on the values of $p$, $q$, and $r$.
- Analyze the fourth expression: $((a ∨ b) ∧ (a → c) ∧ (b → c)) → c$
Using the implication rule, if $a ∨ b$ is true and both $a$ and $b$ imply $c$, then $c$ must be true. This makes the whole expression logically valid.
- Combine the results
Based on individual analyses, we need $r$ to be false if at least one of $p$ or $q$ is true. The second expression is always true, while the first depends on $q$, and the last expression is logically valid.
The answer involves evaluating each expression individually. The simplified form of each expression is as follows:
- For $p ∨ ¬(p ∧ q)$, the truth depends on $q$.
- $(p → q) ↔ (¬p → ¬q)$ is always true.
- $(p ∨ q) → ¬r$ depends on the values of $p$, $q$, and $r$.
- The last expression is logically valid.
More Information
This involves the key concepts of logical expressions and their simplifications. Understanding equivalences, such as contrapositives, is crucial in logic.
Tips
- Confusing the conditional and its contrapositive.
- Misapplying De Morgan's Laws.
- Not considering the truth values properly in implications.
AI-generated content may contain errors. Please verify critical information