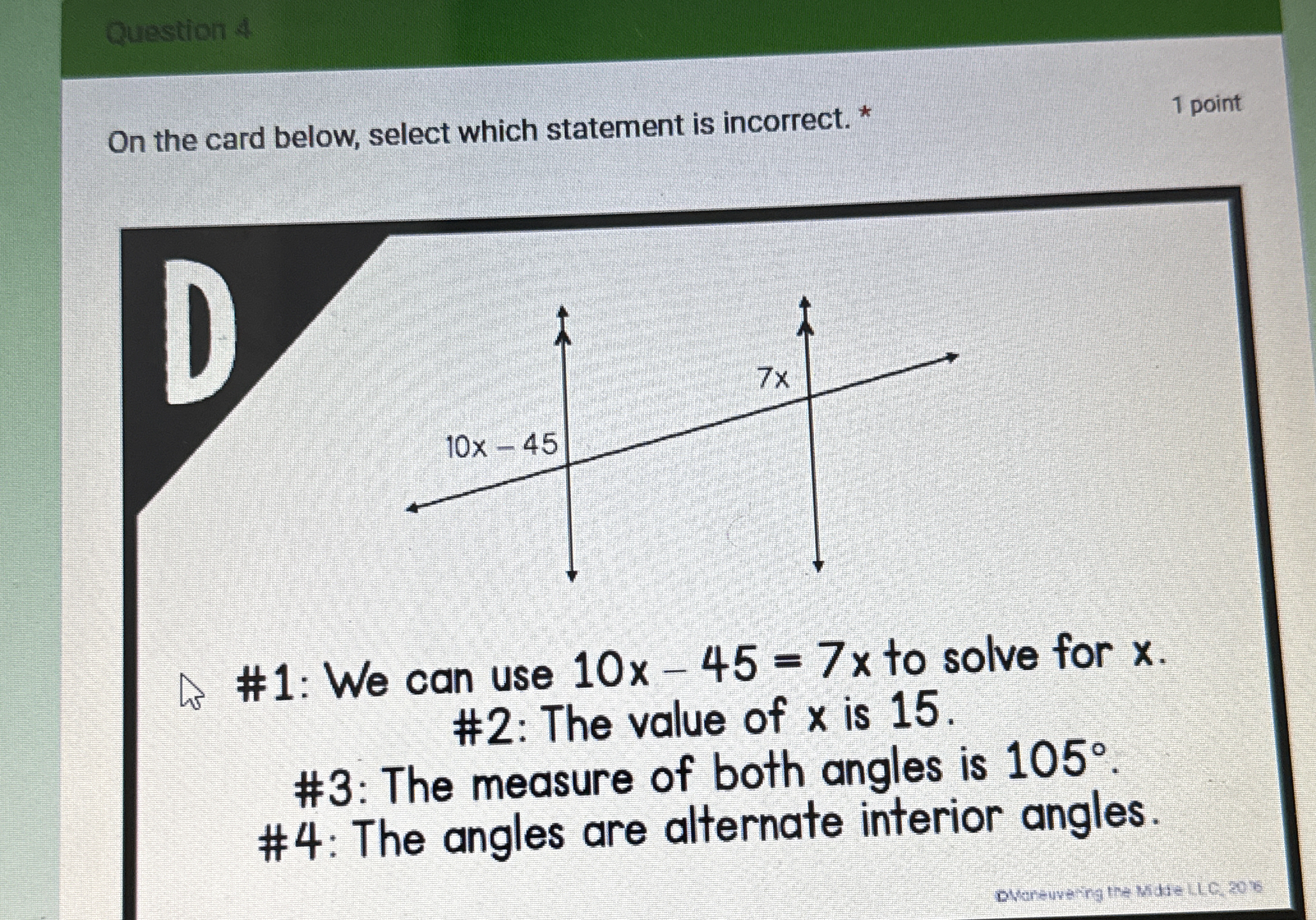
On the card below, select which statement is incorrect: #1: We can use 10x - 45 = 7x to solve for x. #2: The value of x is 15. #3: The measure of both angles is 105°. #4: The angle... On the card below, select which statement is incorrect: #1: We can use 10x - 45 = 7x to solve for x. #2: The value of x is 15. #3: The measure of both angles is 105°. #4: The angles are alternate interior angles. Read more

Steps to Solve

1. Set up the equation The angle expressions given are (10x - 45) and (7x). Since these are alternate interior angles formed by the two lines, we set them equal to each other: $$ 10x - 45 = 7x $$

2. Solve for x To isolate (x), subtract (7x) from both sides: $$ 10x - 7x - 45 = 0 $$ This simplifies to: $$ 3x - 45 = 0 $$ Now add 45 to both sides: $$ 3x = 45 $$ Finally, divide by 3: $$ x = 15 $$

3. Find the angle measures Now substitute (x = 15) back into either angle expression to find the measure of the angles: Using (7x): $$ 7(15) = 105^\circ $$ Using (10x - 45): $$ 10(15) - 45 = 150 - 45 = 105^\circ $$

4. Evaluate the statements Now review each statement:

• Statement 1: Correct, because we solved (10x - 45 = 7x).
• Statement 2: Correct, because we found (x = 15).
• Statement 3: Correct, both angles are indeed (105^\circ).
• Statement 4: Correct, as they are alternate interior angles.

Since all statements are affirmed, we can conclude there is no incorrect statement based on our calculations.