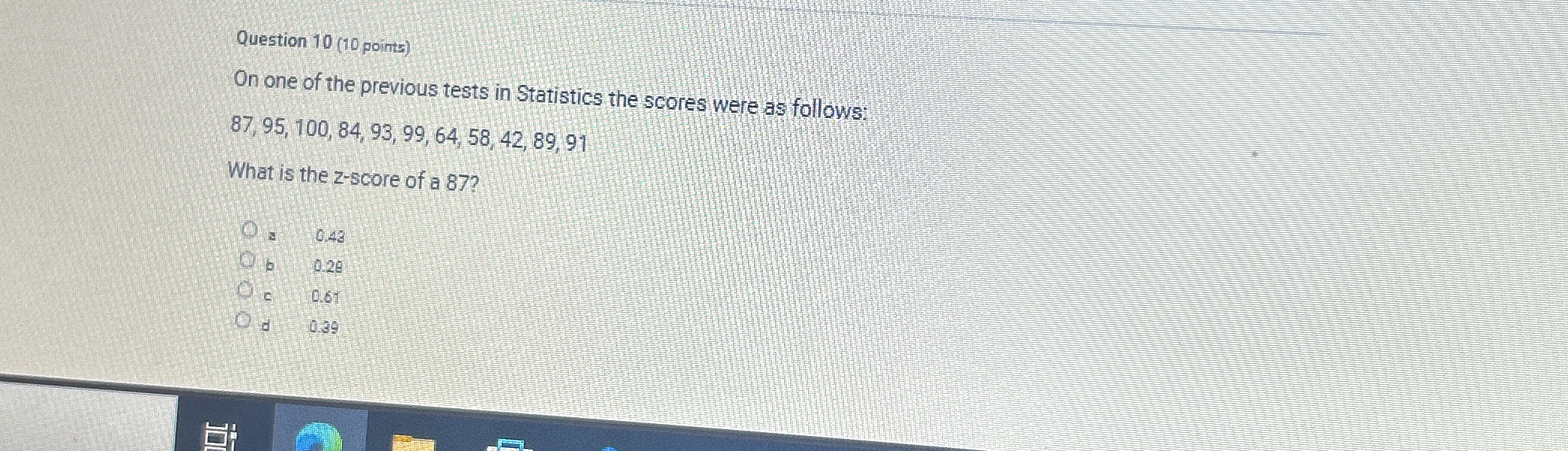
On one of the previous tests in Statistics the scores were as follows: 87, 95, 100, 84, 93, 99, 64, 58, 42, 89, 91. What is the z-score of a 87?

Steps to Solve

1. Calculate the Mean of the Scores
   To find the mean, sum all the scores and divide by the number of scores.
   The scores are: 87, 95, 100, 84, 93, 99, 64, 58, 42, 89, 91.
   Sum of scores:
   $$ 87 + 95 + 100 + 84 + 93 + 99 + 64 + 58 + 42 + 89 + 91 = 1032 $$
   Number of scores: 11
   Mean:
   $$ \text{Mean} = \frac{1032}{11} \approx 93.09 $$

2. Calculate the Standard Deviation
   First, find the variance by calculating the squared differences from the mean, summing them, and dividing by the number of scores.
   The squared differences are:
   $$ (87 - 93.09)^2, (95 - 93.09)^2, (100 - 93.09)^2, (84 - 93.09)^2, (93 - 93.09)^2, $$
   $$ (99 - 93.09)^2, (64 - 93.09)^2, (58 - 93.09)^2, (42 - 93.09)^2, (89 - 93.09)^2, (91 - 93.09)^2 $$
   Calculating these gives us:
   $$ 36.75, 3.61, 47.41, 82.81, 0.01, 34.80, 841.51, 1232.52, 2626.76, 16.80, 4.36 $$
   Sum of squared differences:
   $$ 36.75 + 3.61 + 47.41 + 82.81 + 0.01 + 34.80 + 841.51 + 1232.52 + 2626.76 + 16.80 + 4.36 = 3926.47 $$
   Variance:
   $$ \text{Variance} = \frac{3926.47}{11} \approx 357.86 $$
   Standard Deviation:
   $$ \text{Standard Deviation} = \sqrt{357.86} \approx 18.91 $$

3. Calculate the Z-score for 87
   Use the z-score formula:
   $$ z = \frac{X - \mu}{\sigma} $$
   where $X$ is the score (87), $\mu$ is the mean (93.09), and $\sigma$ is the standard deviation (18.91).
   Substituting the values:
   $$ z = \frac{87 - 93.09}{18.91} \approx \frac{-6.09}{18.91} \approx -0.32 $$