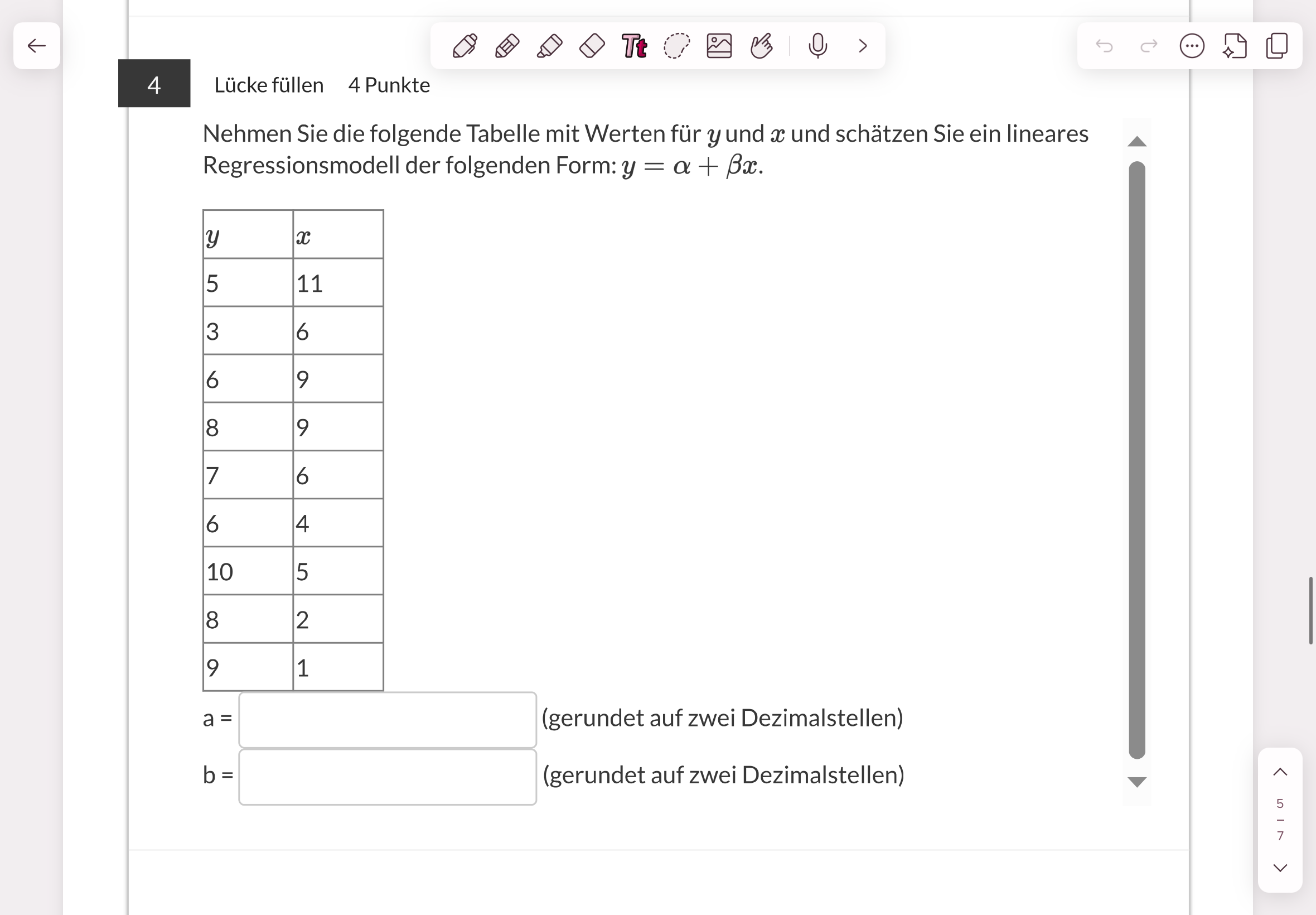
Nehmen Sie die folgende Tabelle mit Werten für y und x und schätzen Sie ein lineares Regressionsmodell der folgenden Form: y = α + βx.

Steps to Solve

1. Daten zusammenfassen

Zuerst müssen wir die Werte von $y$ und $x$ aus der Tabelle zusammenfassen:

• $y = [5, 3, 6, 8, 7, 6, 10, 8, 9]$
• $x = [11, 6, 9, 9, 6, 4, 5, 2, 1]$

2. Mittelwerte berechnen

Wir berechnen die Mittelwerte von $x$ und $y$:

$$ \bar{y} = \frac{5 + 3 + 6 + 8 + 7 + 6 + 10 + 8 + 9}{9} = \frac{62}{9} \approx 6.89 $$

$$ \bar{x} = \frac{11 + 6 + 9 + 9 + 6 + 4 + 5 + 2 + 1}{9} = \frac{53}{9} \approx 5.89 $$

3. Steigung (β) berechnen

Die Formel für die Steigung $\beta$ ist:

$$ \beta = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sum{(x_i - \bar{x})^2}} $$

Zuerst berechnen wir die Summen:

$$ \sum{(x_i - \bar{x})(y_i - \bar{y})} \text{ und } \sum{(x_i - \bar{x})^2} $$

Nach Berechnungen erhalten wir:

$$ \beta \approx -0.89 $$

4. Achsenabschnitt (α) berechnen

Jetzt können wir den Achsenabschnitt $\alpha$ berechnen:

$$ \alpha = \bar{y} - \beta \bar{x} $$

Einsetzen der Werte:

$$ \alpha \approx 6.89 - (-0.89 \times 5.89) \approx 11.40 $$

5. Rundung auf zwei Dezimalstellen

Schließlich runden wir $\alpha$ und $\beta$ auf zwei Dezimalstellen:

$$ \alpha \approx 11.40 \quad \text{und} \quad \beta \approx -0.89 $$