[m^3 n^{-1/4}]^2 ÷ √[5]{32 m^4 n^{-8}}
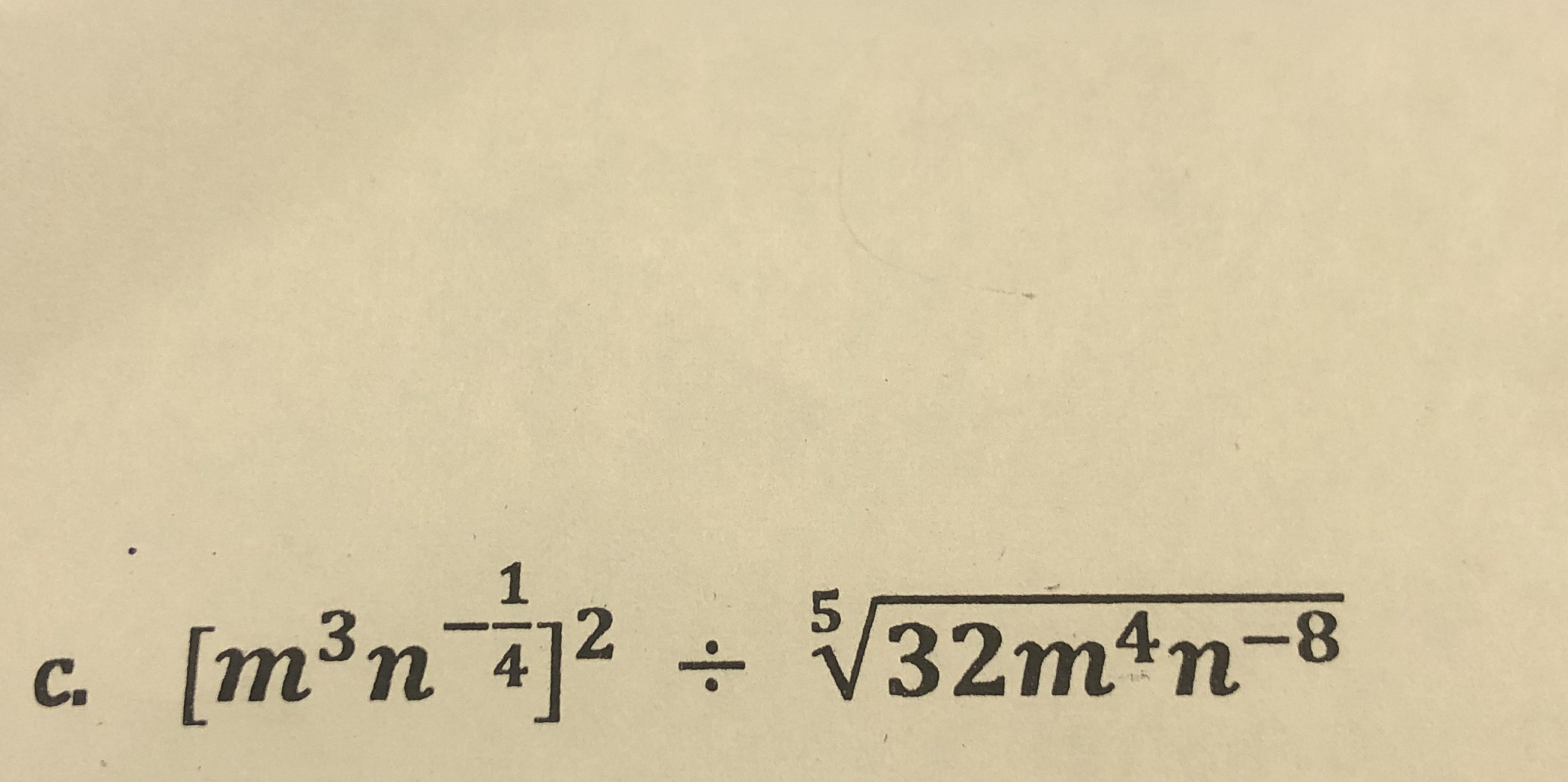
Understand the Problem
The question involves simplifying a mathematical expression that includes exponents, roots, and division. The key concepts include simplification of powers and roots in algebra.
Answer
$$ \frac{m^{\frac{26}{5}} n^{\frac{11}{10}}}{2} $$
Answer for screen readers
The final simplified expression is: $$ \frac{m^{\frac{26}{5}} n^{\frac{11}{10}}}{2} $$
Steps to Solve
-
Simplify the Numerator
We start by simplifying the numerator, which is ( [m^3 n^{-1/4}]^2 ).
Using the power of a power property ( (a^m)^n = a^{mn} ), we have: $$ [m^3 n^{-1/4}]^2 = m^{3 \cdot 2} n^{-1/4 \cdot 2} = m^6 n^{-1/2} $$ -
Simplify the Denominator
Next, we simplify the denominator, which is ( \sqrt[5]{32 m^4 n^{-8}} ).
This can be written as: $$ \sqrt[5]{32} = 32^{1/5} = 2^{5 \cdot 1/5} = 2 $$
So, we have:
$$ \sqrt[5]{32 m^4 n^{-8}} = \sqrt[5]{32} \cdot \sqrt[5]{m^4} \cdot \sqrt[5]{n^{-8}} = 2 m^{4/5} n^{-8/5} $$ -
Set up the Final Expression
Now, substituting the simplified numerator and denominator into the full expression: $$ \frac{m^6 n^{-1/2}}{2 m^{4/5} n^{-8/5}} $$ -
Simplify the Fraction We can now simplify the fraction: $$ = \frac{m^6}{2 m^{4/5}} \cdot \frac{n^{-1/2}}{n^{-8/5}} $$
For the base ( m ): $$ \frac{m^6}{m^{4/5}} = m^{6 - 4/5} = m^{\frac{30}{5} - \frac{4}{5}} = m^{\frac{26}{5}} $$
For the base ( n ): $$ \frac{n^{-1/2}}{n^{-8/5}} = n^{-1/2 + 8/5} = n^{-\frac{5}{10} + \frac{16}{10}} = n^{\frac{11}{10}} $$
So we have: $$ \frac{m^{26/5} n^{11/10}}{2} $$ -
Final Expression
Thus, the simplified expression is: $$ \frac{m^{26/5} n^{11/10}}{2} $$
The final simplified expression is: $$ \frac{m^{\frac{26}{5}} n^{\frac{11}{10}}}{2} $$
More Information
This expression represents the final result after simplifying the original fraction with exponents and roots. The simplification process involves applying exponent rules and careful handling of roots, which is fundamental in algebra.
Tips
- Forgetting to apply exponent rules correctly, particularly when dividing terms with the same base.
- Not simplifying roots properly.
- Miscalculating powers, especially with fractional exponents.
AI-generated content may contain errors. Please verify critical information