Maximize Z = 5x1 + 6x2 Subject to 2x1 + 3x2 ≤ 6, x1, x2 ≥ 0
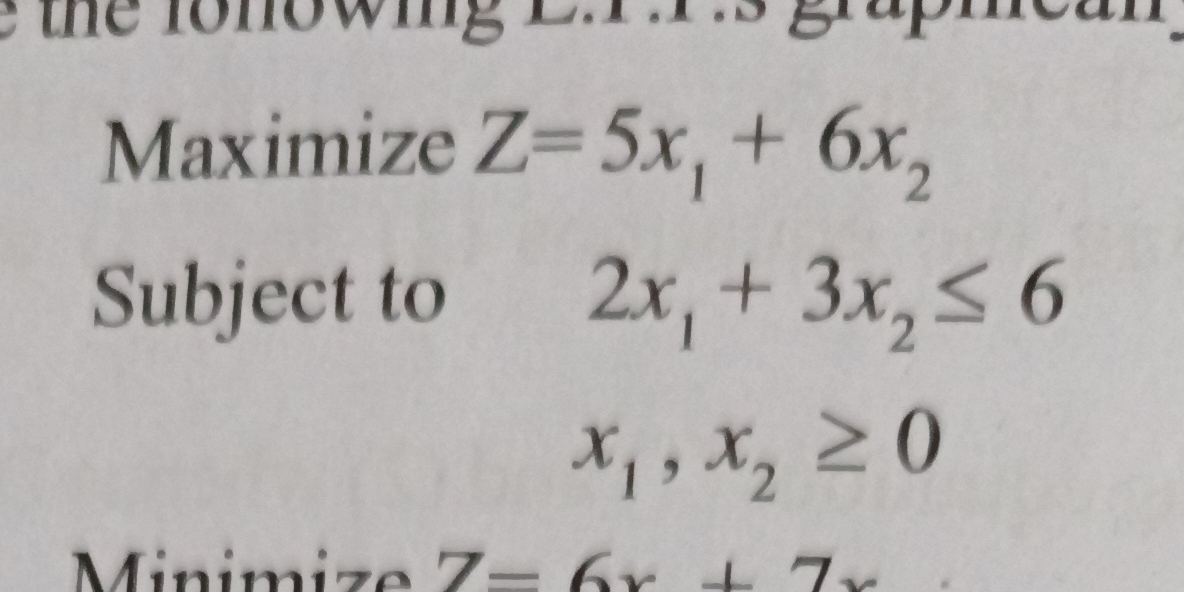
Understand the Problem
The question is asking to graphically solve a linear programming problem, which involves maximizing the objective function Z given subject constraints.
Answer
The maximum value of $Z$ is 15 at the point $(3, 0)$.
Answer for screen readers
The maximum value of $Z$ is $15$ at the point $(3, 0)$.
Steps to Solve
- Identify the constraints and the objective function
The objective function is given by:
$$ Z = 5x_1 + 6x_2 $$
The constraint is:
$$ 2x_1 + 3x_2 \leq 6 $$
Along with the non-negativity constraints:
$$ x_1, x_2 \geq 0 $$
- Convert the inequality into an equation
To find the boundary line of the constraint, we can convert the inequality into an equation:
$$ 2x_1 + 3x_2 = 6 $$
- Determine intercepts of the constraint line
To find the intercepts, set $x_1$ and $x_2$ to zero one at a time:
- For $x_1$-intercept:
Set $x_2 = 0$:
$$ 2x_1 + 3(0) = 6 \implies x_1 = 3 $$
This gives the point $(3, 0)$.
- For $x_2$-intercept:
Set $x_1 = 0$:
$$ 2(0) + 3x_2 = 6 \implies x_2 = 2 $$
This gives the point $(0, 2)$.
- Plot the feasible region
Plot the points $(3, 0)$ and $(0, 2)$ on a graph, and shade the region that satisfies the constraint $2x_1 + 3x_2 \leq 6$ along with the non-negativity restrictions.
- Graph the objective function
Graph the objective function by rearranging it into slope-intercept form:
$$ 6x_2 = Z - 5x_1 $$
For various values of $Z$, determine lines of the form $x_2 = \frac{Z - 5x_1}{6}$.
- Find the optimal solution
Identify the corner points of the feasible region, which are:
- Point A: $(0, 0)$
- Point B: $(3, 0)$
- Point C: $(0, 2)$
- Point D: Intersection of $2x_1 + 3x_2 = 6$ and the axes (not applicable here since we already use intercepts).
Calculate the value of $Z$ at each corner point:
- At $(0, 0)$: $Z = 5(0) + 6(0) = 0$
- At $(3, 0)$: $Z = 5(3) + 6(0) = 15$
- At $(0, 2)$: $Z = 5(0) + 6(2) = 12$
- Select the maximum value
The maximum value of $Z$ occurs at $(3, 0)$, where $Z = 15$.
The maximum value of $Z$ is $15$ at the point $(3, 0)$.
More Information
In linear programming, the solution often occurs at the vertices of the feasible region formed by the constraints. This problem illustrates the graphical method of finding optimal solutions.
Tips
- Not including non-negativity constraints: Always ensure that the solutions also meet $x_1, x_2 \geq 0$.
- Failing to consider boundary points: Always check corner points of the feasible region for maximum or minimum values.
- Incorrectly graphing constraints: Ensure the correct shading of regions under the inequality constraints.
AI-generated content may contain errors. Please verify critical information