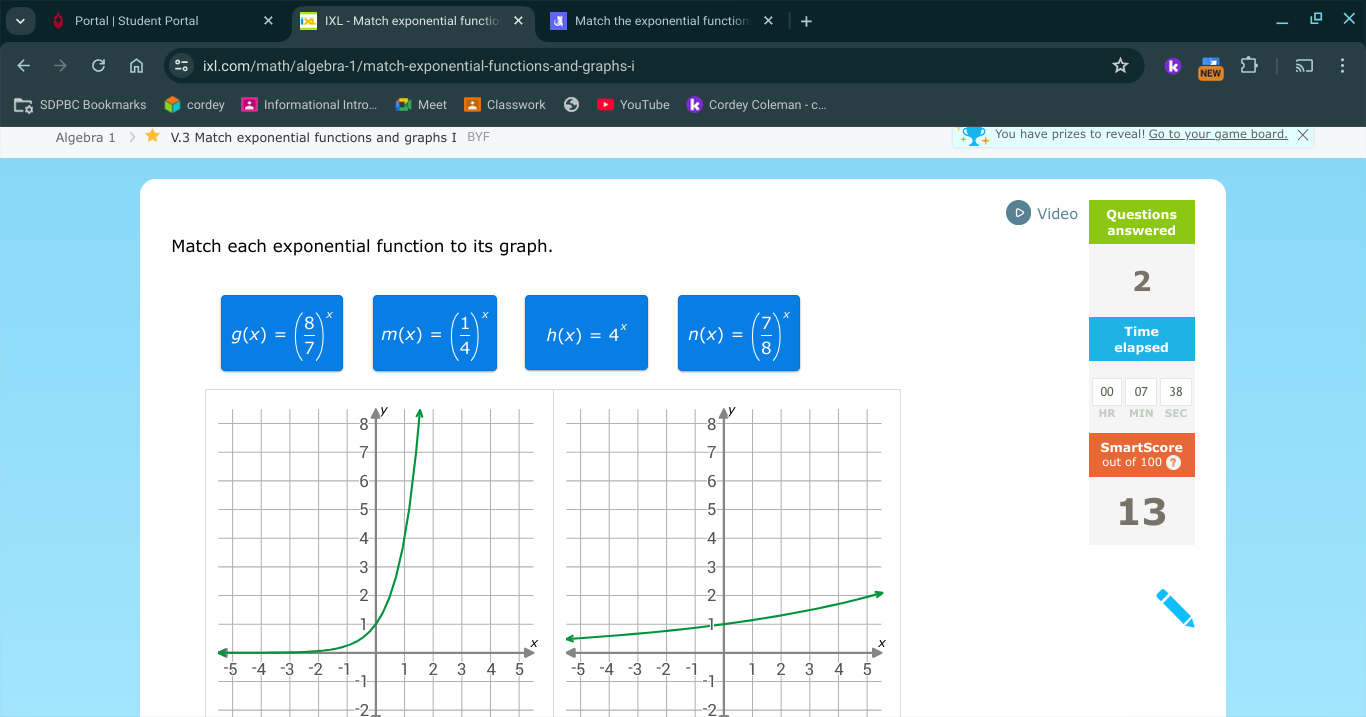
Match each exponential function to its graph.

Steps to Solve

1. Identify the Growth or Decay Type Look at each function and determine if it represents exponential growth or decay.

   • For $g(x) = \left(\frac{8}{7}\right)^x$, the base $\frac{8}{7} > 1$ indicates growth.
   • For $m(x) = \left(\frac{1}{4}\right)^x$, the base $\frac{1}{4} < 1$ indicates decay.
   • For $h(x) = 4^x$, the base $4 > 1$ indicates growth.
   • For $n(x) = \left(\frac{7}{8}\right)^x$, the base $\frac{7}{8} < 1$ indicates decay.

2. Analyze the Graphs Assess the characteristics of the graphs given.

   • The left graph starts low and increases steeply, suggesting exponential growth (possible candidates: $g(x)$ or $h(x)$).
   • The right graph starts higher and decreases gradually, suggesting exponential decay (possible candidates: $m(x)$ or $n(x)$).

3. Match Growth Functions Determine which growth function corresponds to which graph.

   • Between $g(x)$ and $h(x)$, note that $g(x)$ has a base slightly above one ($\frac{8}{7}$) and will grow less aggressively than $h(x) = 4^x$. Therefore, $h(x)$ is expected to rise more steeply, matching with the left graph.

4. Match Decay Functions Determine which decay function corresponds to which graph.

   • Between $m(x)$ and $n(x)$, $m(x) = \left(\frac{1}{4}\right)^x$ decays rapidly because it has a smaller base compared to $n(x) = \left(\frac{7}{8}\right)^x$, which decays more slowly. Therefore, $n(x)$ matches with the right graph.