Let Y1 < Y2 < Y3 < Y4 denote the order statistic of a random sample of size 4 from p.d.f f(x) = e^(-x) for 0 < x < ∞. Find P(Y4 > 3).
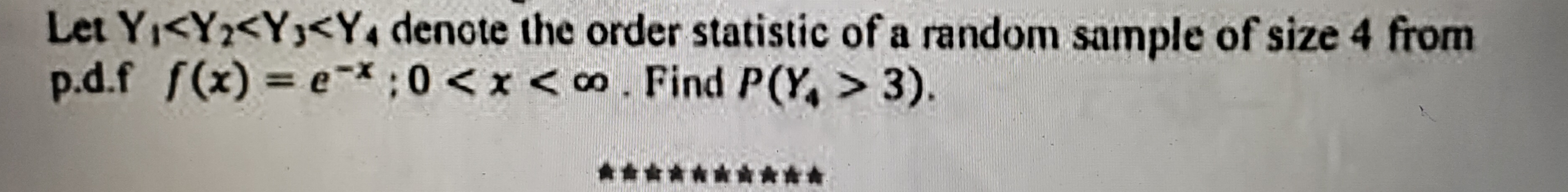
Understand the Problem
The question is asking to find the probability that the highest order statistic (Y4) from a random sample of size 4, drawn from a specified probability density function, is greater than 3. This involves understanding order statistics and applying the cumulative distribution function associated with the given probability density function.
Answer
$$ P(Y_4 > 3) = 1 - (1 - e^{-3})^4 $$
Answer for screen readers
The final answer for ( P(Y_4 > 3) ) is: $$ P(Y_4 > 3) = 1 - (1 - e^{-3})^4 $$
Steps to Solve
-
Understand the Problem We need to find the probability ( P(Y_4 > 3) ), where ( Y_4 ) is the highest order statistic from a sample of size 4.
-
Use the Cumulative Distribution Function (CDF) The given probability density function (pdf) is ( f(x) = e^{-x} ) for ( 0 < x < \infty ). The cumulative distribution function (CDF) is: $$ F(x) = 1 - e^{-x} $$
-
Calculate ( P(Y_4 \leq 3) ) Since ( Y_4 > 3 ) means at least one ( Y_i > 3 ), we can find it using the complement: $$ P(Y_4 > 3) = 1 - P(Y_4 \leq 3) $$
Knowing that ( Y_4 \leq 3 ) means all ( Y_i \leq 3 ): $$ P(Y_4 \leq 3) = P(Y_1 \leq 3) \cdot P(Y_2 \leq 3) \cdot P(Y_3 \leq 3) \cdot P(Y_4 \leq 3) $$
Since each ( Y_i ) is identically distributed: $$ = (P(Y_1 \leq 3))^4 = (F(3))^4 $$
Thus, we compute: $$ P(Y_4 \leq 3) = (1 - e^{-3})^4 $$
-
Calculate Final Probability Now substituting this back: $$ P(Y_4 > 3) = 1 - (1 - e^{-3})^4 $$
The final answer for ( P(Y_4 > 3) ) is: $$ P(Y_4 > 3) = 1 - (1 - e^{-3})^4 $$
More Information
This probability measure indicates the likelihood that the maximum observation in a random sample of four from an exponential distribution exceeds 3. The exponential distribution is often used to model time until an event occurs, such as failure of a system or arrival times in a queue.
Tips
- Not correctly applying the CDF formula; double-check the calculation of ( F(x) ).
- Misunderstanding how to use the complement rule when dealing with order statistics.
- Forgetting that the maximum's distribution is derived from the individual distributions.
AI-generated content may contain errors. Please verify critical information