Let t = -10 - -10. Let v(j) = j^2 + 53j + 285. Let g be v(-47). Solve 0 = -tk - gk for k.

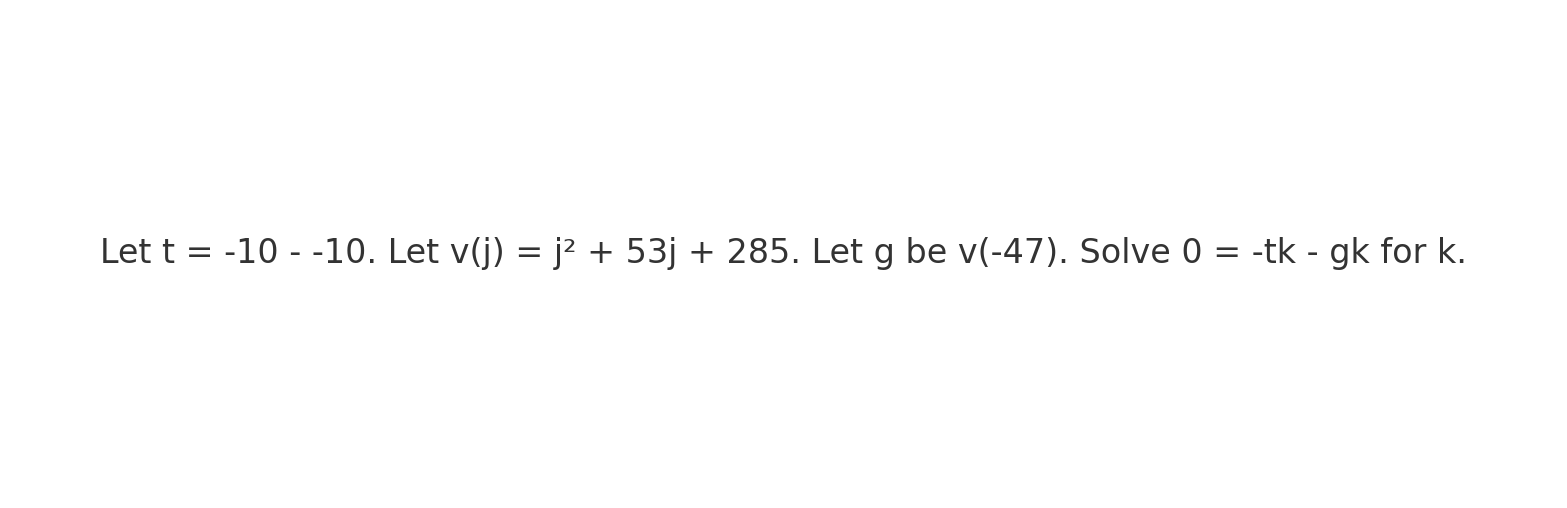
Understand the Problem

The question involves solving an equation related to the variables defined in the context, specifically for the variable k. It requires substituting the given values and simplifying the expression.

Answer

The value of $ k $ is $ k = 0 $.

Steps to Solve

Calculate the value of t To find ( t ), substitute into the equation: $$ t = -10 - (-10) = -10 + 10 = 0 $$
Evaluate the function v(j) at j = -47 Now, substitute ( j = -47 ) into ( v(j) ): $$ v(-47) = (-47)^2 + 53(-47) + 285 $$ Calculating each term:

( (-47)^2 = 2209 )
( 53 \times (-47) = -2491 )

So, $$ v(-47) = 2209 - 2491 + 285 = 2209 - 2491 + 285 = 3 $$

Substitute values into the main equation Now we substitute ( t = 0 ) and ( g = 3 ) into the equation ( 0 = -tk - gk ): $$ 0 = -0 \cdot k - 3k $$ This simplifies to: $$ 0 = -3k $$
Solve for k To find ( k ), isolate it in the equation: $$ -3k = 0 \implies k = 0 $$

The value of ( k ) is ( k = 0 ).

More Information

In this problem, we calculated the value of ( t ), evaluated a quadratic function at a specific point, and then solved a linear equation for ( k ). These types of problems often appear in algebra courses.

Tips

Miscalculating the function ( v(-47) ): Ensure correct arithmetic is used to combine terms.
Forgetting that multiplying by zero results in zero; thus the value ( t ) having no effect on the equation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!