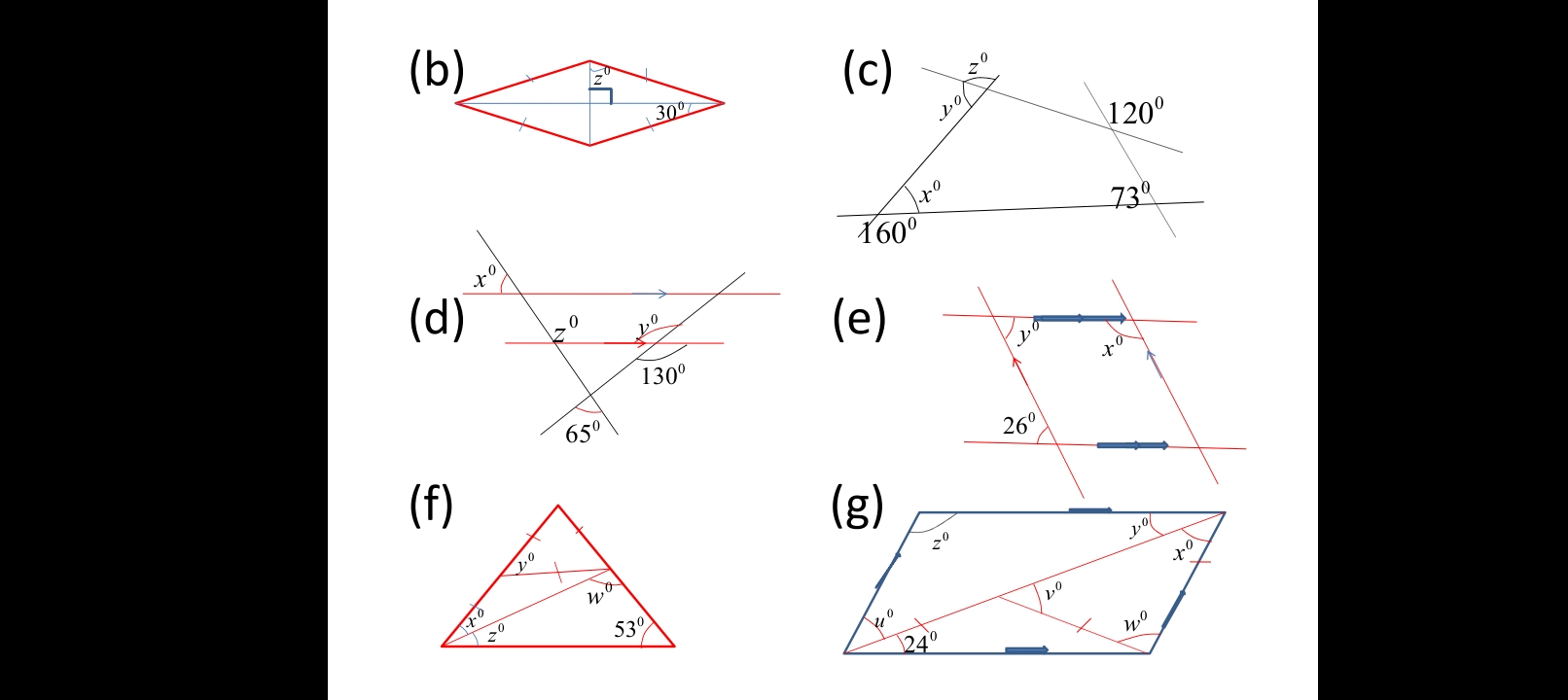
Calculate the values of x°, y°, z°, and w° in the provided geometric figures.

Understand the Problem

The question seeks to solve for the unknown angles labeled as x°, y°, z°, and w° in various geometric figures. This involves applying geometric principles such as the properties of angles, parallel lines, and triangles.

Answer

The angles are: $z^\circ = 30^\circ$, $v^\circ = 60^\circ$, $x^\circ = 60^\circ$, $y^\circ = 50^\circ$, $x^\circ = 77^\circ$, $w^\circ = 50^\circ$, $y^\circ = 26^\circ$, $w^\circ = 77^\circ$, and $y^\circ = 154^\circ$.

Steps to Solve

Calculate angle $z^\circ$ in (b)

In a parallelogram, opposite angles are equal. Thus,

[ z^\circ = 30^\circ ]

Find angle $v^\circ$ in (c)

Using the fact that the sum of angles on a straight line is $180^\circ$, we have:

[ v^\circ + 120^\circ = 180^\circ \implies v^\circ = 60^\circ ]

Determine angle $x^\circ$ in (c)

Since alternate interior angles are equal,

[ x^\circ = 60^\circ ]

Calculate angle $y^\circ$ in (d)

The angles $y^\circ$ and $130^\circ$ are supplementary:

[ y^\circ + 130^\circ = 180^\circ \implies y^\circ = 50^\circ ]

Find angle $x^\circ$ in (f)

Using the triangle sum theorem (the sum of angles in a triangle is $180^\circ$):

[ x^\circ + y^\circ + z^\circ = 180^\circ \implies x^\circ + 50^\circ + 53^\circ = 180^\circ ] [ x^\circ = 77^\circ ]

Calculate angle $w^\circ$ in (f)

Using triangle sum theorem again:

[ w^\circ + 50^\circ + 53^\circ = 180^\circ \implies w^\circ = 77^\circ ]

Find angle $w^\circ$ in (g)

Using properties of angles in a quadrilateral:

[ w^\circ + x^\circ + y^\circ + z^\circ = 360^\circ ] Substituting known angles:

[ w^\circ + 77^\circ + 50^\circ + 24^\circ = 360^\circ \implies w^\circ = 209^\circ ]

Determine angle $y^\circ$ in (e)

Using the properties of parallel lines:

[ y^\circ = 26^\circ ]

Calculate angle $v^\circ$ in (e)

Using the opposite angles theorem:

[ v^\circ = 154^\circ ]

The angles are:

$z^\circ = 30^\circ$
$v^\circ = 60^\circ$
$x^\circ = 60^\circ$
$y^\circ = 50^\circ$
$x^\circ = 77^\circ$ (in triangle f)
$w^\circ = 50^\circ$
$y^\circ = 26^\circ$ (in e)
$w^\circ = 77^\circ$ (in f)
$y^\circ = 154^\circ$ (in e)

More Information

These angles are derived using properties of angles in parallelograms, triangles, and relationships involving parallel lines and transversal segments.

Tips

Confusing alternate interior angles with corresponding angles.
Forgetting that the sum of angles in a triangle must equal $180^\circ$.
Miscalculating supplementary angles (the sum must be $180^\circ$).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!