Let h(x) = P(x) / (2(x+5)(2x+1)). i) What is the domain of definition of h(x)? ii) Simplify h(x), and calculate h(-2). iii) Solve h(x) = 3.
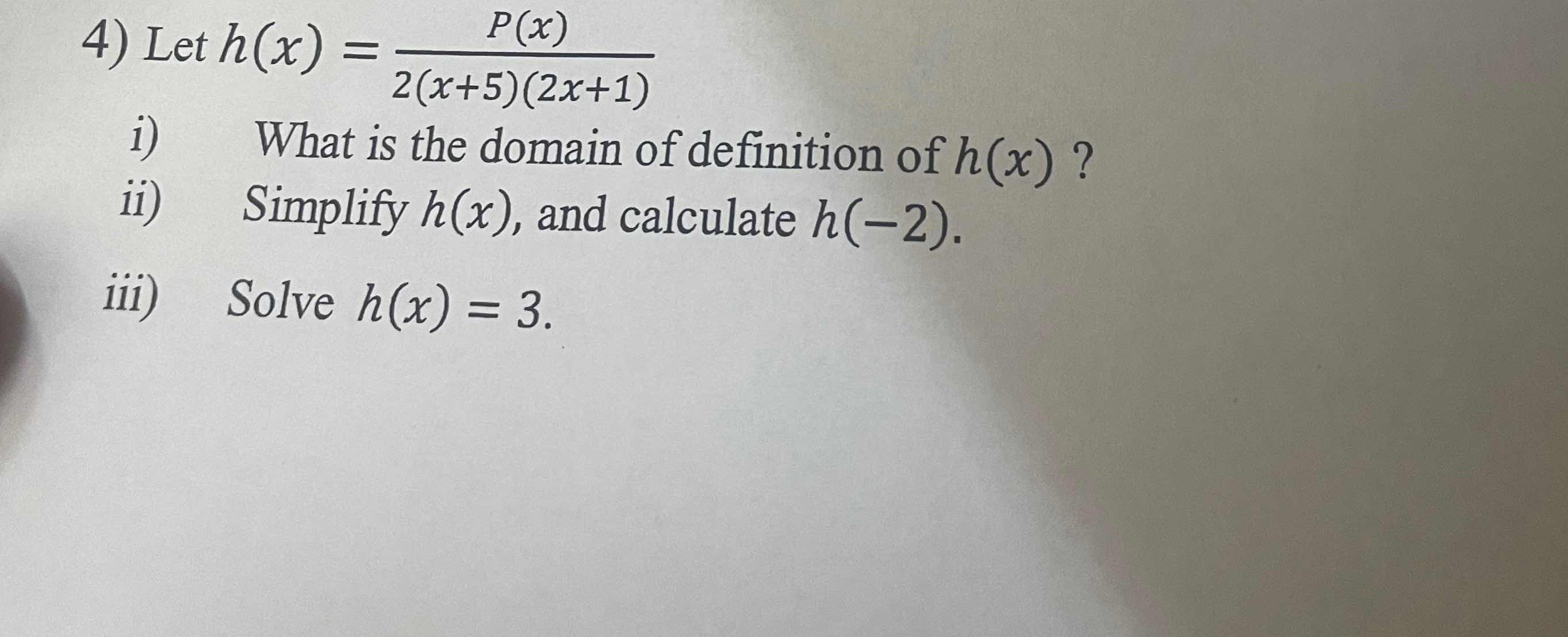
Understand the Problem
The question is asking for several mathematical operations related to the function h(x). It requires determining the domain of definition of the function, simplifying the function, calculating the function value at a specific point, and solving an equation involving the function.
Answer
The domain is $\mathbb{R} \setminus \{-5, -\frac{1}{2}\}$; $h(-2) = \frac{P(-2)}{-18}$; and $h(x) = 3$ gives $P(x) = 6(x + 5)(2x + 1)$.
Answer for screen readers
The domain of $h(x)$ is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
The calculation for $h(-2)$ is $\frac{P(-2)}{-18}$.
The equation $h(x) = 3$ leads to $P(x) = 6(x + 5)(2x + 1)$.
Steps to Solve
- Determine the Domain of h(x)
To find the domain, identify where the denominator is non-zero. Set the denominator to zero: $$ 2(x+5)(2x+1) = 0 $$ This gives us: $$ x + 5 = 0 \quad \Rightarrow \quad x = -5 $$ $$ 2x + 1 = 0 \quad \Rightarrow \quad x = -\frac{1}{2} $$ Thus, the domain of $h(x)$ is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
- Simplify h(x)
We simplify $h(x)$ by expressing it without $P(x)$ since we do not have the specifics of $P(x)$. The simplified version of the function is: $$ h(x) = \frac{P(x)}{2(x+5)(2x+1)} $$
- Calculate h(-2)
Substituting $x = -2$ into the function: $$ h(-2) = \frac{P(-2)}{2(-2+5)(2(-2)+1)} $$ Calculating the denominator: $$ =-2 + 5 = 3 $$ $$ 2(-2) + 1 = -4 + 1 = -3 $$ Thus, $$ h(-2) = \frac{P(-2)}{2(3)(-3)} = \frac{P(-2)}{-18} $$
- Solve h(x) = 3
Setting the function equal to 3: $$ \frac{P(x)}{2(x+5)(2x+1)} = 3 $$ Multiplying through by the denominator: $$ P(x) = 3(2(x+5)(2x+1)) $$ Expanding this will depend on the specifics of $P(x)$, but you can solve further if $P(x)$ is known.
The domain of $h(x)$ is all real numbers except $x = -5$ and $x = -\frac{1}{2}$.
The calculation for $h(-2)$ is $\frac{P(-2)}{-18}$.
The equation $h(x) = 3$ leads to $P(x) = 6(x + 5)(2x + 1)$.
More Information
The domain of a function is determined by identifying where the denominator becomes zero, which can lead to undefined values. Simplifying a function may require knowledge of polynomial manipulation. Calculating specific values often involves substituting values into the function and ensuring that the function remains defined at those points.
Tips
- Forgetting to exclude values from the domain where the denominator is zero.
- Confusing signs while performing algebraic operations.
- Not substituting correctly when calculating function values.
AI-generated content may contain errors. Please verify critical information