Let b = x, d = 2x. S = mg(1/3) / (4/4*J) for rectangle. I = bd^3 / 12. S = mg(1/3)*X/ (4*Y*bd^3). Case for (a) where b = 2x, d = x. I1 = mg(1/3) / (4*Y*2x^3).
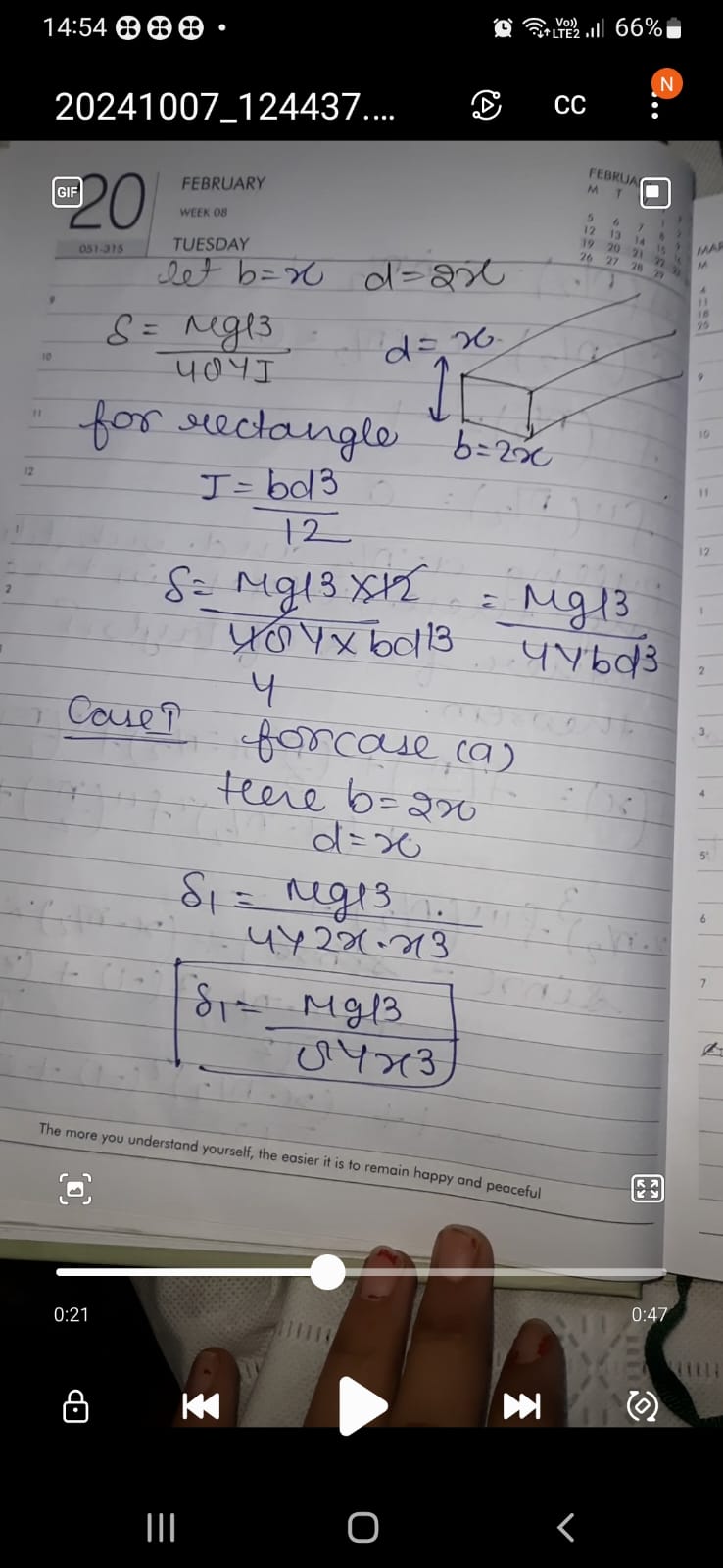
Understand the Problem
The question involves solving a mathematical problem concerning dimensions of a rectangular prism. It defines variables for the base and depth (width and height) using 'x' and '2x', incorporates physical principles as well as equations related to volume or force and may involve simplifying the equations.
Answer
$$ S = \frac{mgX}{8Yx^4}, \quad S_1 = \frac{mg(1/3)}{8Yx^4} $$
Answer for screen readers
For the first case, the stress is: $$ S = \frac{mgX}{8Yx^4} $$
For case (a), the stress is: $$ S_1 = \frac{mg(1/3)}{8Yx^4} $$
Steps to Solve
-
Identify Variables Given:
- Base ( b = x )
- Depth ( d = 2x )
-
Write the Formula for the Moment of Inertia (I) The formula for the moment of inertia for a rectangular prism is given by: $$ I = \frac{bd^3}{12} $$ Substitute ( b ) and ( d ): $$ I = \frac{x(2x)^3}{12} = \frac{x(8x^3)}{12} $$
-
Simplify the Moment of Inertia (I) Simplifying the obtained formula gives: $$ I = \frac{8x^4}{12} = \frac{2x^4}{3} $$
-
Calculate Stress (S) From the problem, the formula for stress is: $$ S = \frac{mg(1/3) \cdot X}{(4 \cdot Y) \cdot I} $$ Substitute ( I ): $$ S = \frac{mg(1/3) \cdot X}{(4 \cdot Y) \cdot \left(\frac{2x^4}{3}\right)} $$
-
Simplify the Stress Equation Simplifying provides: $$ S = \frac{mg(1/3) \cdot X \cdot 3}{4Y \cdot 2x^4} = \frac{mgX}{8Yx^4} $$
-
Case for (a) For the case where ( b = 2x ) and ( d = x ) repeat the process: Substitute ( b ) and ( d ) into the moment of inertia: $$ I_1 = \frac{(2x)(x^3)}{12} = \frac{2x^4}{12} = \frac{x^4}{6} $$
-
Calculate ( S_1 ) for Case (a) Using the stress formula: $$ S_1 = \frac{mg(1/3)}{4Y \cdot (2x)(x^3)} $$ Simplifying gives: $$ S_1 = \frac{mg(1/3)}{8Yx^4} $$
For the first case, the stress is: $$ S = \frac{mgX}{8Yx^4} $$
For case (a), the stress is: $$ S_1 = \frac{mg(1/3)}{8Yx^4} $$
More Information
This problem involves concepts of stress and the moment of inertia in material mechanics. The formulas show how geometric dimensions affect the behavior of materials under load.
Tips
- Forgetting to correctly substitute and simplify variables throughout calculations can lead to errors.
- Not accounting for units consistently, which can affect the final results.
AI-generated content may contain errors. Please verify critical information