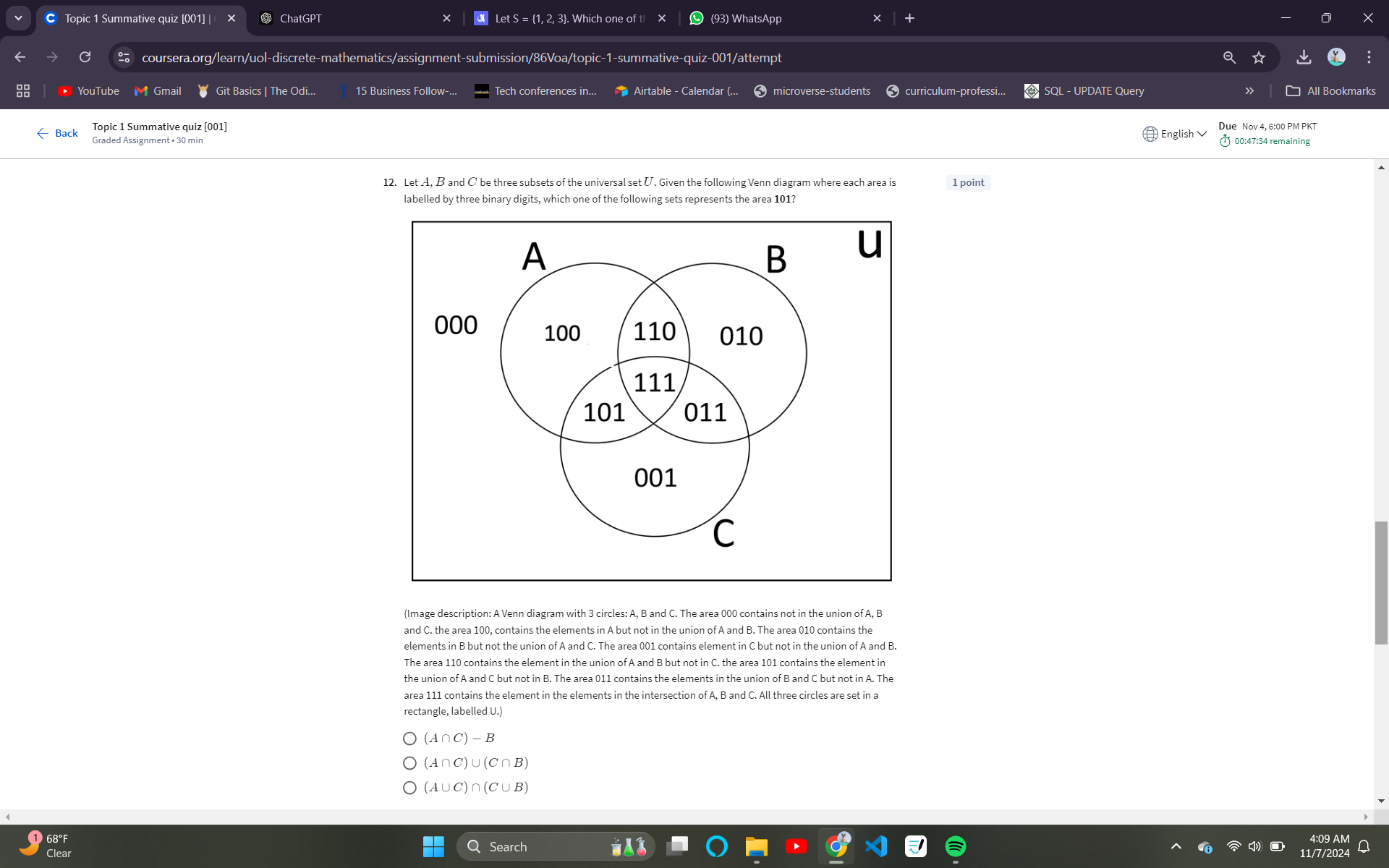
Let A, B and C be three subsets of the universal set U. Given the following Venn diagram where each area is labelled by three binary digits, which one of the following sets represe... Let A, B and C be three subsets of the universal set U. Given the following Venn diagram where each area is labelled by three binary digits, which one of the following sets represents the area 101?
Understand the Problem
The question is asking to identify which set expression corresponds to the area labeled '101' in the provided Venn diagram that represents sets A, B, and C. It requires understanding of set operations and how they relate to the Venn diagram.
Answer
The expression for area '101' is \( (A \cap C) - B \).
Answer for screen readers
The expression that corresponds to the area '101' is ( (A \cap C) - B ).
Steps to Solve
- Identifying the Area '101' in the Venn Diagram
The area labeled '101' corresponds to elements that are:
- In set A (because the first digit is 1)
- Not in set B (because the second digit is 0)
- In set C (because the third digit is 1)
- Translating the Area into Set Operations
From the above identification, we can express the area '101' using set operations:
- The element is in A and C but not in B.
This can be written as: $$ A \cap C \cap B' $$ where $B'$ denotes the complement of set B (i.e., not in B).
- Comparing with the Given Options
Now, check the provided options against our expression:
- Option 1: ( (A \cap C) - B ) represents ( A \cap C \cap B' ), which matches our expression.
After evaluating the other options, they do not yield the same combination of sets as '101'.
The expression that corresponds to the area '101' is ( (A \cap C) - B ).
More Information
In set notation, ( A \cap B ) denotes the intersection of sets A and B, while ( A - B ) or ( A \cap B' ) denotes the elements in A that are not in B. The area '101' illustrates elements within A and C but excludes any from B, making it a typical application of set intersections and differences.
Tips
- Overlooking the complement: Be careful not to confuse the elements that are included or excluded based on their presence in sets.
- Misunderstanding intersection and union: Remember that intersection (∩) requires elements to be in both sets, while union (∪) combines all elements from both sets.
AI-generated content may contain errors. Please verify critical information