f(x) = √(x² - 1)

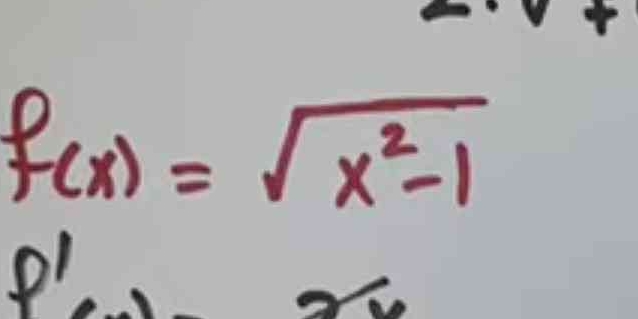
Understand the Problem

The question involves analyzing a mathematical function f(x) expressed as the square root of (x^2 - 1). It appears to be a calculus-related question that may require finding the derivative or understanding its properties.

Answer

The derivative is $f'(x) = \frac{x}{\sqrt{x^2 - 1}}$.

Steps to Solve

Identify the function The function given is $f(x) = \sqrt{x^2 - 1}$.
Apply the Chain Rule To differentiate the function, we will use the Chain Rule. The Chain Rule states that if you have a composite function $f(g(x))$, its derivative is $f'(g(x)) \cdot g'(x)$.
Find the outer and inner functions Here, let the outer function $f(u) = \sqrt{u}$, where $u = x^2 - 1$. We need to find $f'(u)$ and $g'(x)$.
Differentiate the outer function The derivative of the outer function is given by: $$ f'(u) = \frac{1}{2\sqrt{u}} = \frac{1}{2\sqrt{x^2 - 1}} $$
Differentiate the inner function Now, for the inner function $g(x) = x^2 - 1$, we find its derivative: $$ g'(x) = 2x $$
Combine using the Chain Rule Now, apply the Chain Rule: $$ f'(x) = f'(g(x)) \cdot g'(x) = \frac{1}{2\sqrt{x^2 - 1}} \cdot 2x $$
Simplify the expression This simplifies to: $$ f'(x) = \frac{x}{\sqrt{x^2 - 1}} $$

The derivative of the function $f(x) = \sqrt{x^2 - 1}$ is given by:

$$ f'(x) = \frac{x}{\sqrt{x^2 - 1}} $$

More Information

The function $f(x) = \sqrt{x^2 - 1}$ represents the upper half of a hyperbola. Its derivative shows the rate of change and is only defined for $|x| \geq 1$, where the square root is real.

Tips

Forgetting the Chain Rule: Many students miss applying the Chain Rule when differentiating composite functions.
Incorrect simplification: Be careful when simplifying fractions, particularly when involving square roots.
Ignoring the domain: Remember the function's restriction: it is only defined for $|x| \geq 1$.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!