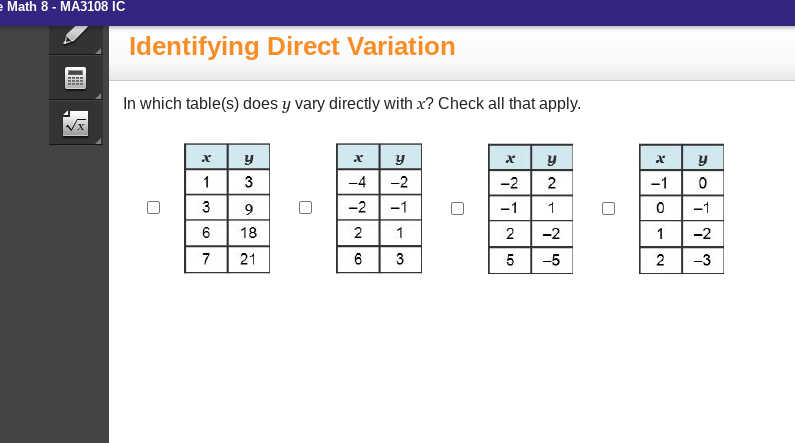
In which table(s) does y vary directly with x? Check all that apply.

Understand the Problem

The question is asking which tables demonstrate direct variation between the variables x and y. Direct variation occurs when y can be expressed as a constant multiple of x. To identify this, we need to analyze the ratios of y to x for each table and check if they remain consistent.

Answer

The tables demonstrating direct variation are: Table 1, Table 2, Table 3.

Steps to Solve

Identify the ratio in each table

For each table, calculate the ratio of $y$ to $x$. This ratio should be constant for direct variation.

Calculate the ratios for Table 1

In Table 1:

For $(1, 3)$: $y/x = 3/1 = 3$
For $(3, 9)$: $y/x = 9/3 = 3$
For $(6, 18)$: $y/x = 18/6 = 3$
For $(7, 21)$: $y/x = 21/7 = 3$

The ratio is constant at $3$.

Calculate the ratios for Table 2

In Table 2:

For $(-4, -2)$: $y/x = -2/-4 = 0.5$
For $(-2, -1)$: $y/x = -1/-2 = 0.5$
For $(2, 1)$: $y/x = 1/2 = 0.5$
For $(6, 3)$: $y/x = 3/6 = 0.5$

The ratio is constant at $0.5$.

Calculate the ratios for Table 3

In Table 3:

For $(-2, 2)$: $y/x = 2/-2 = -1$
For $(-1, 1)$: $y/x = 1/-1 = -1$
For $(2, -2)$: $y/x = -2/2 = -1$
For $(5, -5)$: $y/x = -5/5 = -1$

The ratio is constant at $-1$.

Calculate the ratios for Table 4

In Table 4:

For $(-1, 0)$: Not a valid ratio (undefined).
For $(0, -1)$: Not a valid ratio (undefined).
For $(1, -2)$: $y/x = -2/1 = -2$
For $(2, -3)$: $y/x = -3/2 = -1.5$

The ratios are not consistent.

The tables that demonstrate direct variation are Table 1, Table 2, and Table 3.

More Information

Direct variation essentially means that as one variable changes, the other changes in a consistent, proportional way. The key indicator is that the ratio of the two variables remains the same across all values in the table.

Tips

Failing to simplify the ratios correctly can lead to incorrect conclusions about whether there is direct variation.
Misapplying direct variation by not checking all values in the table can result in overlooking valid consistent ratios.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!