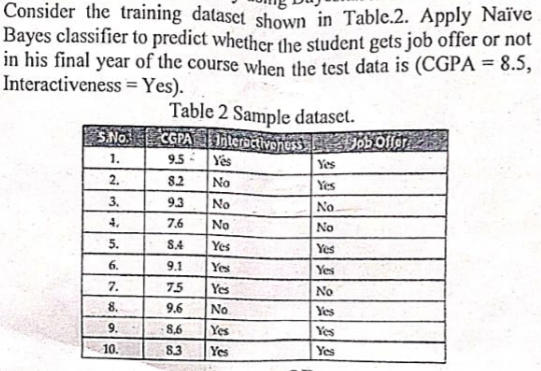
Consider the training dataset shown in Table 2. Apply Naïve Bayes classifier to predict whether the student gets job offer or not in his final year of the course when the test data... Consider the training dataset shown in Table 2. Apply Naïve Bayes classifier to predict whether the student gets job offer or not in his final year of the course when the test data is (CGPA = 8.5, Interactiveness = Yes). Read more

Steps to Solve

1. Calculating Prior Probabilities

First, we need to calculate the prior probabilities for the classes (Job Offer: Yes or No):

• Number of instances with Job Offer = Yes: 5
• Number of instances with Job Offer = No: 5

The total number of instances is 10.

Thus, the prior probabilities are:

$$ P(\text{Yes}) = \frac{5}{10} = 0.5 $$

$$ P(\text{No}) = \frac{5}{10} = 0.5 $$

2. Calculating Conditional Probabilities

Next, calculate the conditional probabilities for CGPA and Interactiveness:

For CGPA:

• We assume a Gaussian distribution for CGPA. Calculate the mean and standard deviation of CGPA for both classes.

For Class "Yes":

• CGPAs: 9.5, 8.4, 9.1, 9.6, 8.6

Mean:

$$ \mu_{\text{Yes}} = \frac{9.5 + 8.4 + 9.1 + 9.6 + 8.6}{5} = \frac{45.2}{5} = 9.04 $$

Standard Deviation:

$$ \sigma_{\text{Yes}} = \sqrt{\frac{(9.5 - 9.04)^2 + (8.4 - 9.04)^2 + (9.1 - 9.04)^2 + (9.6 - 9.04)^2 + (8.6 - 9.04)^2}{5}} $$

Calculating this will yield approximately:

$$ \sigma_{\text{Yes}} \approx 0.435 $$

For Class "No":

• CGPAs: 8.2, 9.3, 7.6, 7.5, 8.3

Mean:

$$ \mu_{\text{No}} = \frac{8.2 + 9.3 + 7.6 + 7.5 + 8.3}{5} = \frac{40.9}{5} = 8.18 $$

Standard Deviation:

$$ \sigma_{\text{No}} = \sqrt{\frac{(8.2 - 8.18)^2 + (9.3 - 8.18)^2 + (7.6 - 8.18)^2 + (7.5 - 8.18)^2 + (8.3 - 8.18)^2}{5}} $$

Calculating this will yield approximately:

$$ \sigma_{\text{No}} \approx 0.456 $$

For Interactiveness:

• Yes (Job Offer = Yes): Count = 5
• No (Job Offer = Yes): Count = 0

Thus:

$$ P(\text{Yes | Interactiveness=Yes}) = \frac{5}{5} = 1 $$

$$ P(\text{No | Interactiveness=Yes}) = \frac{0}{5} = 0 $$

3. Applying Gaussian Probability Density Function (PDF)

Calculate the Gaussian PDF for CGPA = 8.5 under each class:

For Yes:

$$ P(\text{CGPA=8.5 | Yes}) = \frac{1}{\sigma_{\text{Yes}} \sqrt{2\pi}} e^{-\frac{(8.5 - \mu_{\text{Yes}})^2}{2\sigma_{\text{Yes}}^2}} $$

Substituting our values:

$$ P(\text{CGPA=8.5 | Yes}) \approx \frac{1}{0.435 \sqrt{2\pi}} e^{-\frac{(8.5 - 9.04)^2}{2 \cdot (0.435)^2}} $$

For No:

$$ P(\text{CGPA=8.5 | No}) = \frac{1}{\sigma_{\text{No}} \sqrt{2\pi}} e^{-\frac{(8.5 - \mu_{\text{No}})^2}{2\sigma_{\text{No}}^2}} $$

Substituting our values:

$$ P(\text{CGPA=8.5 | No}) \approx \frac{1}{0.456 \sqrt{2\pi}} e^{-\frac{(8.5 - 8.18)^2}{2 \cdot (0.456)^2}} $$

4. Calculation of Posterior Probabilities

Now, calculate:

$$ P(\text{Yes | Data}) = P(\text{CGPA=8.5 | Yes}) \cdot P(\text{Yes | Interactiveness=Yes}) $$

$$ P(\text{No | Data}) = P(\text{CGPA=8.5 | No}) \cdot P(\text{No | Interactiveness=Yes}) $$

Since ( P(\text{No | Interactiveness=Yes}) = 0 ), we only need ( P(\text{Yes | Data}) ).

5. Final Prediction

Determine which posterior probability is higher:

If ( P(\text{Yes | Data}) > P(\text{No | Data}) ): Predict "Yes" Else: Predict "No"