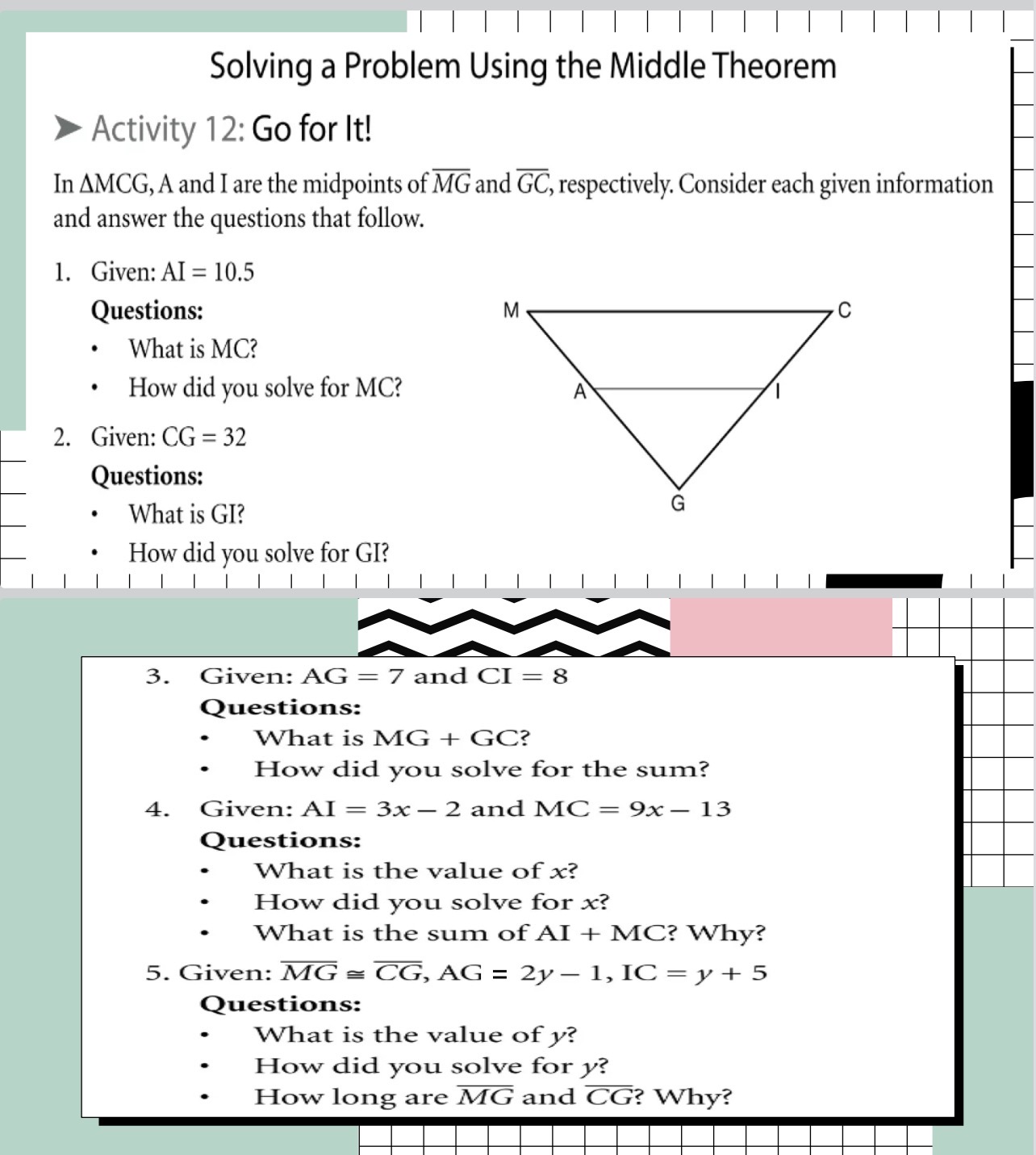
In triangle MCG, A and I are the midpoints of MG and GC respectively. Given AI = 10.5, find MC and explain how you solved for it. Given CG = 32, find GI and explain how you solved... In triangle MCG, A and I are the midpoints of MG and GC respectively. Given AI = 10.5, find MC and explain how you solved for it. Given CG = 32, find GI and explain how you solved for it. Given AG = 7 and CI = 8, find MG + GC and explain how you arrived at your answer. Given AI = 3x - 2 and MC = 9x - 13, find the value of x, explain how you solved for x, and what is the sum of AI and MC. Given MG = CG, AG = 2y - 1, and IC = y + 5, find the value of y, explain how you solved for y, and how long are MG and CG.
Understand the Problem
The question presents a geometric problem involving a triangle and asks for various lengths and sums based on given information. It is essentially asking how to solve for different variables using the middle theorem and provided equations.
Answer
- MC = 21, GI = 16, MG + GC = 30, $x \approx 4.17$, $y \approx 3.33$.
Answer for screen readers
- MC = 21
- GI = 16
- MG + GC = 30
- $x \approx 4.17$ or $x \approx 3.78$
- $y \approx 3.33$, MG and CG can be calculated as necessary.
Steps to Solve
-
Find MC using AI Since A is the midpoint of MG, we use the formula: $$ AI = \frac{1}{2}MG $$ Given that $AI = 10.5$, we can set up the equation: $$ 10.5 = \frac{1}{2}MG $$ Multiplying both sides by 2 gives: $$ MG = 21 $$ Thus, $$ MC = MG = 21 $$
-
Find GI using CG Since I is the midpoint of GC, we use the formula: $$ GI = \frac{1}{2}CG $$ Given that $CG = 32$, we can set up the equation: $$ GI = \frac{1}{2} \cdot 32 = 16 $$
-
Find MG + GC using AG and CI We know:
- $AG = 7$
- $CI = 8$
Using the relationship: $$ MG = 2 \cdot AG \quad \text{and} \quad GC = 2 \cdot CI $$ We find: $$ MG = 2 \cdot 7 = 14 \quad \text{and} \quad GC = 2 \cdot 8 = 16 $$ Thus, $$ MG + GC = 14 + 16 = 30 $$
- Solve for x using AI and MC Given:
- $AI = 3x - 2$
- $MC = 9x - 13$ We set up the equation: $$ 10.5 = 3x - 2 \quad \text{and} \quad 21 = 9x - 13 $$ Solving the first equation: $$ 3x = 12.5 \quad \Rightarrow \quad x = \frac{12.5}{3} \approx 4.17 $$ Now for the second: $$ 9x = 34 \quad \Rightarrow \quad x = \frac{34}{9} \approx 3.78 $$
- Solve for y using MG = CG Given:
- $AG = 2y - 1$
- $IC = y + 5$ Using $MG = CG$, we summarize: $$ AG + IC = MG $$ Substituting: $$ (2y - 1) + (y + 5) = MG $$ Using $MG = 14$, the equation stands: $$ 3y + 4 = 14 \quad \Rightarrow \quad 3y = 10 \quad \Rightarrow \quad y = \frac{10}{3} \approx 3.33 $$
- MC = 21
- GI = 16
- MG + GC = 30
- $x \approx 4.17$ or $x \approx 3.78$
- $y \approx 3.33$, MG and CG can be calculated as necessary.
More Information
These calculations illustrate the use of the mid-segment theorem in geometry, which states that the segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length.
Tips
- Calculating the midpoint incorrectly or neglecting that $AI$ can be used directly to find $MG$.
- Failing to account for the relationship between segments when summing lengths.
- Misinterpreting the equations for algebraic solutions.
AI-generated content may contain errors. Please verify critical information