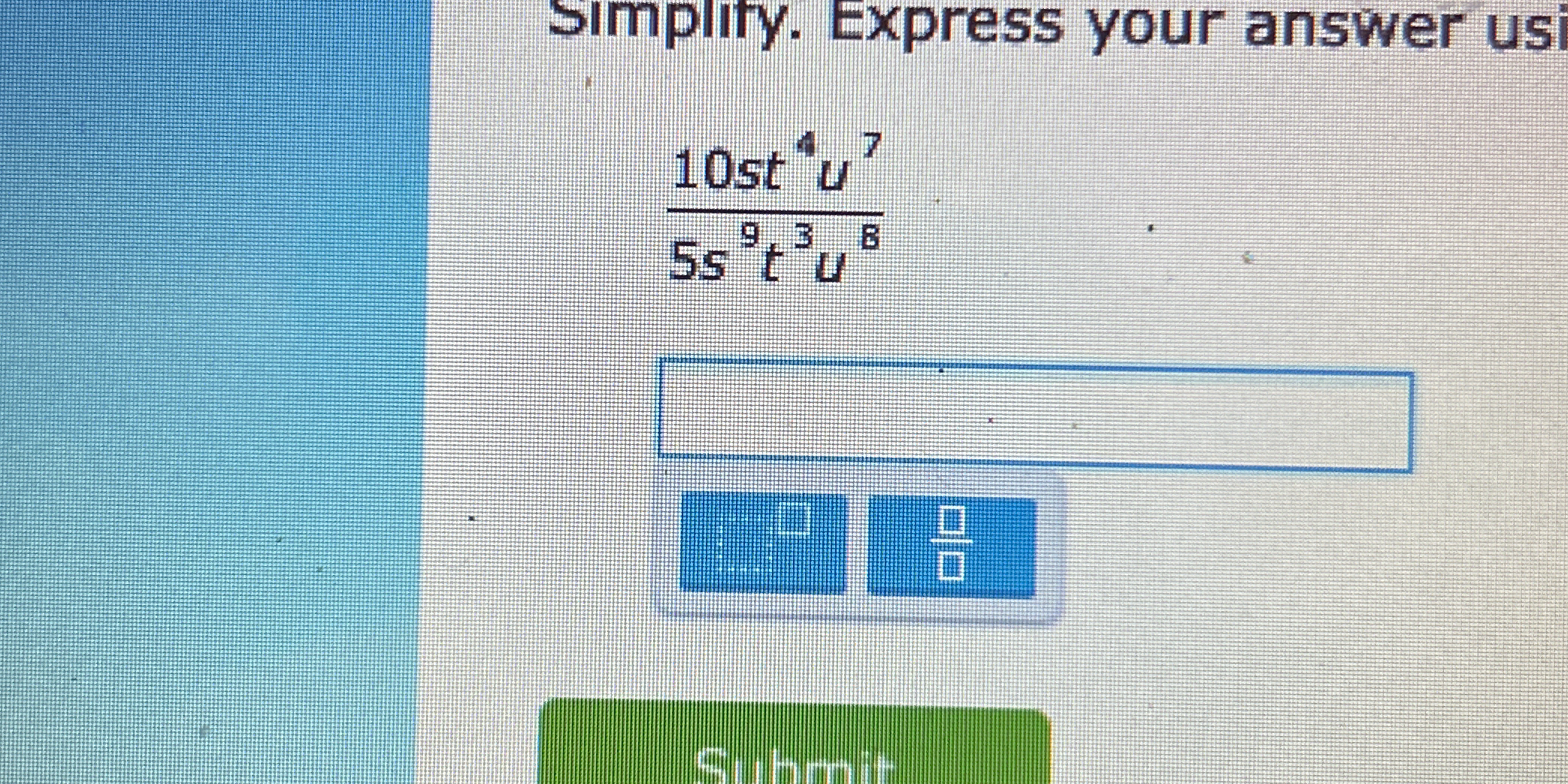
Simplify. Express your answer using the following: (10s^4 t^7)/(5s^9 t^3 u^8)
Understand the Problem
The question is asking to simplify the mathematical expression involving variables and numbers. It consists of a fraction where both the numerator and the denominator contain variable terms raised to different powers. The goal is to simplify this fraction by applying the laws of exponents and algebra.
Answer
$$ \frac{2t^4}{s^5} $$
Answer for screen readers
The simplified expression is:
$$ \frac{2t^4}{s^5} $$
Steps to Solve
-
Simplify the coefficients
First, we simplify the numerical coefficients in the fraction:
$$ \frac{10}{5} = 2 $$ -
Simplify the variable $s$
Next, we simplify the $s$ terms using the rule $a^m / a^n = a^{m-n}$:
$$ \frac{s^4}{s^9} = s^{4-9} = s^{-5} $$ -
Simplify the variable $t$
Now, we simplify the $t$ terms:
$$ \frac{t^7}{t^3} = t^{7-3} = t^4 $$ -
Simplify the variable $u$
For $u$, we have:
$$ \frac{u^1}{u^1} = u^{1-1} = u^0 = 1 $$ -
Combine the simplified components
Putting all the parts together:
$$ 2s^{-5}t^4 $$ -
Rewrite the expression
We can write $s^{-5}$ as $\frac{1}{s^5}$:
$$ 2 \cdot \frac{t^4}{s^5} = \frac{2t^4}{s^5} $$
The simplified expression is:
$$ \frac{2t^4}{s^5} $$
More Information
In this simplification, we used the properties of exponents to manage the variables effectively. Understanding the laws of exponents is crucial for simplifying expressions like these.
Tips
- Confusing $a^m \cdot a^n$ with $a^{m+n}$ instead of using $a^m / a^n = a^{m-n}$ for division.
- Forgetting to simplify the coefficients before handling the variables.
- Not recognizing that $u^1/u^1$ equals $1$.
AI-generated content may contain errors. Please verify critical information