In the given figure, l is parallel to m. Find x.
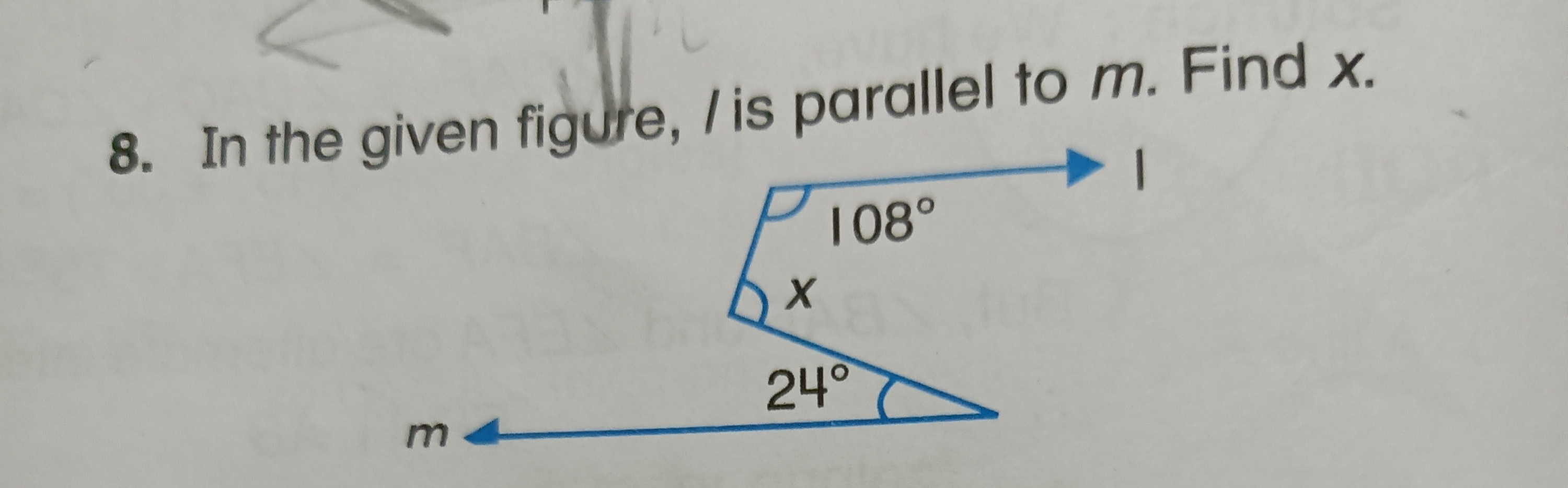
Understand the Problem
The question is asking to find the value of 'x' in a geometrical figure where two lines are parallel and several angles are given. We will use the properties of angles formed by parallel lines and a transversal to solve for 'x'.
Answer
$x = 72^\circ$
Answer for screen readers
The value of $x$ is $72^\circ$.
Steps to Solve
-
Identify Angle Relationships Since lines $l$ and $m$ are parallel, the angles can be related using properties of parallel lines. The angle $108^\circ$ is an exterior angle to the transversal and is adjacent to angle $x$.
-
Use the Linear Pair Postulate The angles on a straight line sum up to $180^\circ$. Therefore, we can write the equation: $$ 108^\circ + x = 180^\circ $$ This equation accounts for the straight line formed by the angles.
-
Solve for x Rearranging the equation: $$ x = 180^\circ - 108^\circ $$
Now, perform the subtraction: $$ x = 72^\circ $$
-
Verify with the Other Angle Additionally, the angle formed with $x$ and the angle $24^\circ$ below $x$ also provides a relationship since they are on the same transversal: $$ x + 24^\circ = 180^\circ $$ Check this for consistency: $$ 72^\circ + 24^\circ = 96^\circ \quad \text{(Not relevant since $108^\circ$ was used)} $$
The value of $x$ is $72^\circ$.
More Information
The problem utilizes the properties of angles formed by a transversal intersecting parallel lines. Understanding these properties helps in solving various geometry problems involving parallel lines and angle relationships.
Tips
- Confusing the relationships between different angles; it's essential to accurately identify which angles form linear pairs or alternate interior angles.
- Not accounting for both angles aligned to the same transversal can lead to incomplete solutions.
AI-generated content may contain errors. Please verify critical information