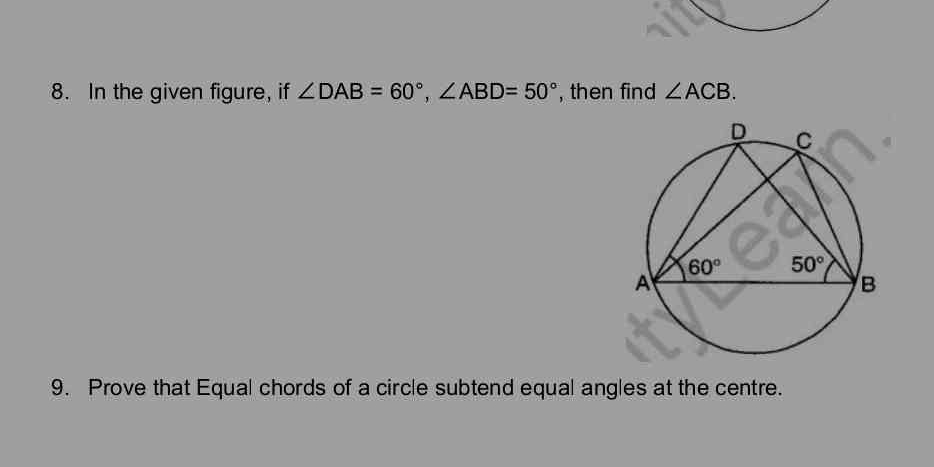
In the given figure, if ∠DAB = 60°, ∠ABD = 50°, then find ∠ACB. Prove that equal chords of a circle subtend equal angles at the centre.
Understand the Problem
The questions are asking to solve angle relationships in a geometric figure. The first question involves determining the angle ∠ACB using the given angles ∠DAB and ∠ABD, while the second question requires a proof related to equal chords of a circle subtending equal angles at the center.
Answer
The angle $\angle ACB$ is $110^\circ$.
Answer for screen readers
The angle $\angle ACB$ is $110^\circ$.
Steps to Solve
-
Identify the relationship between angles
We know that in triangle $ABD$, the sum of the angles should equal $180^\circ$. Therefore:
$$ \angle DAB + \angle ABD + \angle ADB = 180^\circ $$ -
Substitute known values
Substituting the known angles into the equation:
$$ 60^\circ + 50^\circ + \angle ADB = 180^\circ $$ -
Calculate the angle ADB
Now we can solve for $\angle ADB$:
$$ \angle ADB = 180^\circ - 60^\circ - 50^\circ $$
$$ \angle ADB = 70^\circ $$ -
Use the Exterior Angle Theorem
Next, apply the Exterior Angle Theorem where $\angle ACB$ is an exterior angle to triangle $ABD$:
$$ \angle ACB = \angle DAB + \angle ABD $$ -
Substitute values to find ACB
Substituting the values we have:
$$ \angle ACB = 60^\circ + 50^\circ $$
$$ \angle ACB = 110^\circ $$ -
Conclude the proof for equal chords
To prove that equal chords subtend equal angles at the center, consider two equal chords $AB$ and $CD$, with both subtending angles $\theta$ at the center. This leads to the conclusion that if two chords are equal, then the angles subtended by these chords at the center of the circle must also be equal.
The angle $\angle ACB$ is $110^\circ$.
More Information
When two angles are known in a triangle, the third angle can easily be found using the sum of angles property. Also, equal chords imply equal subtended angles at the center, which is an essential property in circle geometry.
Tips
- Confusing Exterior and Interior Angles: Remember that exterior angles equal the sum of the opposite interior angles.
- Wrongly assuming angle relationships: Ensure all angle measures are calculated using the triangle sum property correctly.
AI-generated content may contain errors. Please verify critical information