10 log{(10)^(70/10) + (10)^(70/10)}
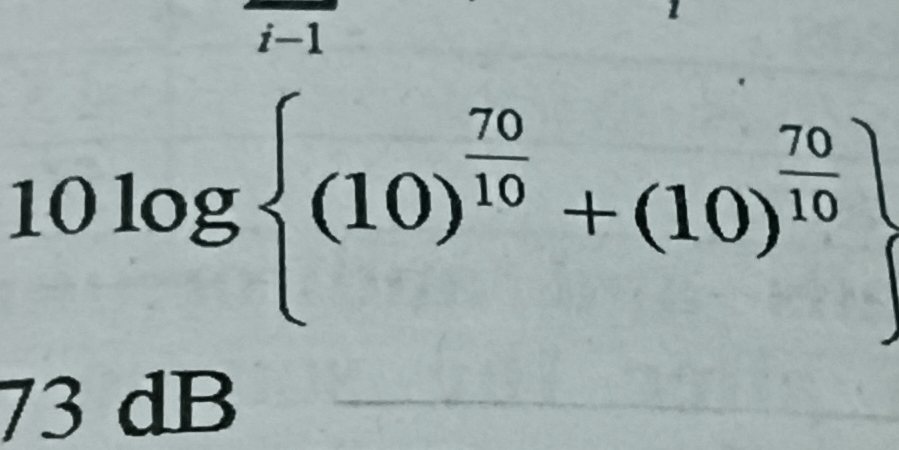
Understand the Problem
The question involves an expression in logarithmic form and seems to require evaluation of the equation, which likely relates to calculations involving decibels or power levels.
Answer
The final answer is approximately $73.010 \, \text{dB}$.
Answer for screen readers
The final answer is approximately $73.010 , \text{dB}$.
Steps to Solve
- Evaluate the exponents
First, simplify the terms inside the logarithm. Use the formula for exponents:
$$ (10)^{\frac{70}{10}} = (10)^{7} = 10^7 $$
So, we have:
$$ (10)^{\frac{70}{10}} + (10)^{\frac{70}{10}} = 10^7 + 10^7 $$
- Combine the terms
Now combine the like terms:
$$ 10^7 + 10^7 = 2 \times 10^7 $$
- Apply the logarithm
Next, apply the logarithm to the expression:
$$ 10 \log(2 \times 10^7) $$
Using the logarithmic property:
$$ \log(ab) = \log(a) + \log(b) $$
We can break it down:
$$ 10 \log(2) + 10 \log(10^7) $$
Since $ \log(10^7) = 7 $, we have:
$$ 10 \log(2) + 10 \cdot 7 $$
- Calculate the values
Now, we can simplify further:
$$ 10 \log(2) + 70 $$
The numerical value of $ \log(2) \approx 0.3010$, so:
$$ 10 \cdot 0.3010 + 70 = 3.010 + 70 $$
- Final calculation
Combine the values to get the final answer:
$$ 3.010 + 70 = 73.010 $$
The final answer is approximately $73.010 , \text{dB}$.
More Information
This calculation is commonly used in acoustics and telecommunications, where decibels (dB) are used to measure signal levels. The logarithmic scale allows for a more manageable representation of large numbers, especially in power and intensity measurements.
Tips
- Forgetting to apply logarithmic properties correctly, especially when combining logarithmic terms.
- Miscalculating the logarithm of 10, which leads to errors in final calculations.
- Not simplifying terms correctly before applying logarithms.
AI-generated content may contain errors. Please verify critical information