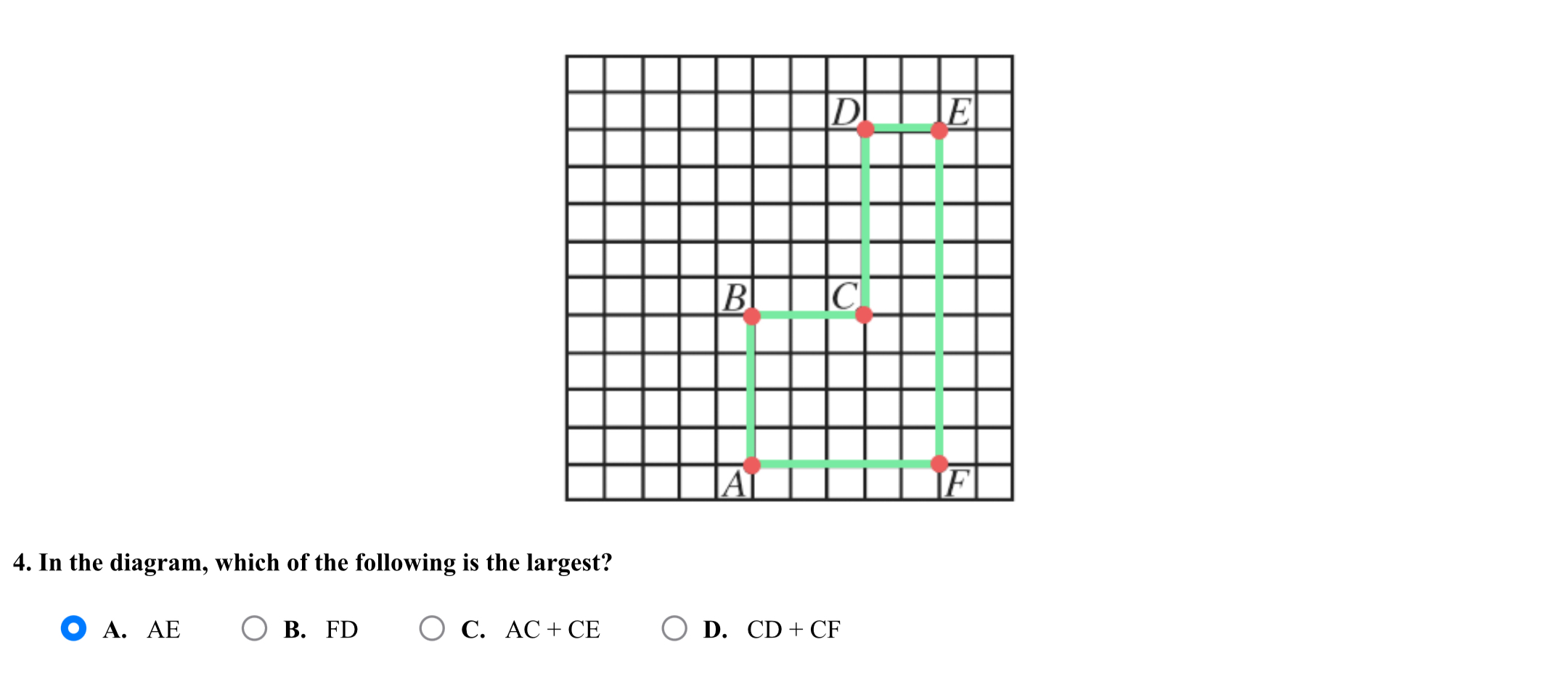
In the diagram, which of the following is the largest?

Steps to Solve

1. Calculate Length of Segment AE Identify the coordinates of points A and E:

   • A (0, 2)
   • E (5, 4)

   Use the distance formula: $$ \text{Length} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$ Calculate: $$ AE = \sqrt{(5 - 0)^2 + (4 - 2)^2} = \sqrt{5^2 + 2^2} = \sqrt{25 + 4} = \sqrt{29} $$

2. Calculate Length of Segment FD Identify the coordinates of points F and D:

   • F (2, 0)
   • D (5, 4)

   Calculate: $$ FD = \sqrt{(5 - 2)^2 + (4 - 0)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$

3. Calculate Length of Segment AC + CE Identify the lengths:

   • AC (from A to C)
   • C (1, 2)
   • E (5, 4)

   First calculate AC: $$ AC = \sqrt{(1 - 0)^2 + (2 - 2)^2} = \sqrt{1} = 1 $$

   Now calculate CE: $$ CE = \sqrt{(5 - 1)^2 + (4 - 2)^2} = \sqrt{4^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20} $$

   Total length: $$ AC + CE = 1 + \sqrt{20} $$

4. Calculate Length of Segment CD + CF Identify the lengths:

   • C (1, 2)
   • D (5, 4)
   • F (2, 0)

   First calculate CD: $$ CD = \sqrt{(5 - 1)^2 + (4 - 2)^2} = \sqrt{4^2 + 2^2} = \sqrt{16 + 4} = \sqrt{20} $$

   Now calculate CF: $$ CF = \sqrt{(2 - 1)^2 + (0 - 2)^2} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} $$

   Total length: $$ CD + CF = \sqrt{20} + \sqrt{5} $$

5. Compare All Lengths Now we compare:

   • Length of AE: $\sqrt{29}$
   • Length of FD: $5$
   • Length of AC + CE: $1 + \sqrt{20}$
   • Length of CD + CF: $\sqrt{20} + \sqrt{5}$

   Estimate the square roots:

   • $\sqrt{20} \approx 4.47$
   • $\sqrt{29} \approx 5.38$
   • $\sqrt{5} \approx 2.24$

   Comparison:

   • AE: $\sqrt{29} \approx 5.38$
   • FD: $5$
   • AC + CE: $1 + 4.47 \approx 5.47$
   • CD + CF: $4.47 + 2.24 \approx 6.71$