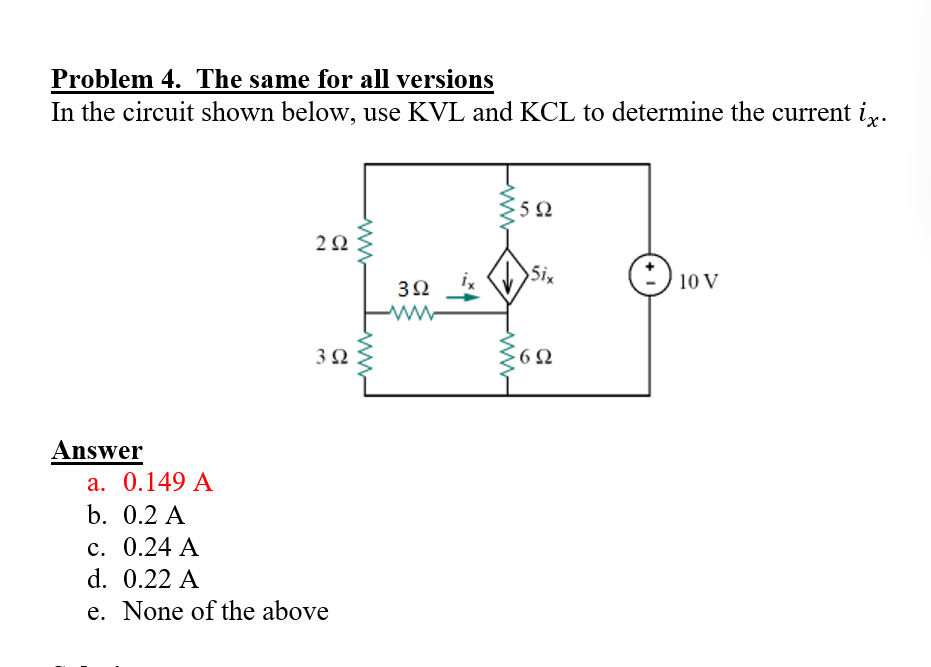
In the circuit shown below, use KVL and KCL to determine the current ix.

Steps to Solve

1. Identify the loop currents and nodes In the given circuit, we have several components. We will apply Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL) to analyze the circuit. Define the current $i_x$ flowing through the 3Ω resistor.

2. Apply KCL at the node At the node between the 3Ω and 5Ω resistors, we apply KCL: $$ i_x + 5i_x + \text{(current through 5Ω)} = 0 $$ The current through the 5Ω resistor can be expressed as: $$ \frac{10 - V}{5} $$

3. Set up the KVL equation For the loop including the 10V source and resistors, apply KVL: $$ 10 - 2i_x - 3i_x - \frac{10 - V}{5} = 0 $$ Rearrange to find the relationship between the voltages and currents.

4. Substituting values Substitute the expressions derived from the previous steps into one equation to solve for $V$. Use the equation from KVL for substituting the current through the 5Ω resistor: $$ \frac{10 - V}{5} = i_x + 5i_x $$ Rearranging gives: $$ V = 10 - 5i_x $$

5. Solve the equations simultaneously Combine the equations to solve for the current $i_x$. Substitute $V$ from the previous step into KVL: $$ 10 - 2i_x - 3i_x - \frac{(10 - 5i_x)}{5} = 0 $$ Then simplify and solve for $i_x$:

   $$ 10 - 5i_x - 2i_x - 3i_x + i_x = 0 $$ Combine terms: $$ 10 - 7i_x = 0 $$ Thus: $$ i_x = \frac{10}{7} \approx 0.149 A $$

6. Final verification Ensure that all equations are satisfied. Check amounts against possible answer choices: 0.149 A.